Soluzioni per la sfida del generatore di serie numeriche - Parte 5

Questa è la quinta e ultima parte della serie che copre le soluzioni alla sfida del generatore di serie numeriche. Nella parte 1, parte 2, parte 3 e parte 4 ho trattato soluzioni T-SQL pure. All'inizio, quando ho pubblicato il puzzle, diverse persone hanno commentato che la soluzione con le migliori prestazioni sarebbe probabilmente quella basata su CLR. In questo articolo metteremo alla prova questo presupposto intuitivo. In particolare, tratterò le soluzioni basate su CLR pubblicate da Kamil Kosno e Adam Machanic.

Mille grazie ad Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea e Paul White per aver condiviso idee e commenti.

Farò i miei test in un database chiamato testdb. Utilizza il codice seguente per creare il database se non esiste e per abilitare le statistiche di I/O e tempo:

-- DB and stats
SET NOCOUNT ON;
SET STATISTICS IO, TIME ON;
GO
 
IF DB_ID('testdb') IS NULL CREATE DATABASE testdb;
GO
 
USE testdb;
GO

Per semplicità, disabiliterò la sicurezza rigorosa CLR e renderò il database affidabile utilizzando il seguente codice:

-- Enable CLR, disable CLR strict security and make db trustworthy
EXEC sys.sp_configure 'show advanced settings', 1;
RECONFIGURE;
 
EXEC sys.sp_configure 'clr enabled', 1;
EXEC sys.sp_configure 'clr strict security', 0;
RECONFIGURE;
 
EXEC sys.sp_configure 'show advanced settings', 0;
RECONFIGURE;
 
ALTER DATABASE testdb SET TRUSTWORTHY ON; 
GO

Soluzioni precedenti

Prima di trattare le soluzioni basate su CLR, esaminiamo rapidamente le prestazioni di due delle soluzioni T-SQL più performanti.

La soluzione T-SQL più performante che non utilizzava tabelle di base persistenti (a parte la tabella columnstore vuota fittizia per ottenere l'elaborazione batch) e quindi non comportava operazioni di I/O, è stata quella implementata nella funzione dbo.GetNumsAlanCharlieItzikBatch. Ho trattato questa soluzione nella Parte 1.

Ecco il codice per creare la tabella columnstore vuota fittizia utilizzata dalla query della funzione:

DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO

Ed ecco il codice con la definizione della funzione:

CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Per prima cosa testiamo la funzione che richiede una serie di 100 milioni di numeri, con l'aggregato MAX applicato alla colonna n:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Ricordiamo, questa tecnica di test evita di trasmettere 100 milioni di righe al chiamante ed evita anche lo sforzo in modalità riga coinvolto nell'assegnazione delle variabili quando si utilizza la tecnica di assegnazione delle variabili.

Ecco le statistiche temporali che ho ottenuto per questo test sulla mia macchina:

L'esecuzione di questa funzione non produce letture logiche, ovviamente.

Quindi, testiamolo con ordine, usando la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

Ricordiamo che questa funzione non comporta l'ordinamento quando si richiedono i dati ordinati per n; in pratica ottieni lo stesso piano indipendentemente dal fatto che tu richieda o meno i dati ordinati. Possiamo attribuire la maggior parte del tempo extra in questo test rispetto al precedente alle assegnazioni di variabili basate su modalità riga da 100 milioni.

La soluzione T-SQL con le migliori prestazioni che utilizzava una tabella di base persistente, e quindi produceva alcune operazioni di I/O, sebbene molto poche, era la soluzione di Paul White implementata nella funzione dbo.GetNums_SQLkiwi. Ho trattato questa soluzione nella parte 4.

Ecco il codice di Paul per creare sia la tabella columnstore utilizzata dalla funzione che la funzione stessa:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Per prima cosa testiamolo senza ordine utilizzando la tecnica aggregata, risultando in un piano in modalità batch:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Ho ottenuto le seguenti statistiche di tempo e I/O per questa esecuzione:

Testiamo la funzione con ordine usando la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

Come per la soluzione precedente, anche questa soluzione evita l'ordinamento esplicito nel piano, e quindi ottiene lo stesso piano indipendentemente dal fatto che tu richieda o meno i dati ordinati. Ma ancora una volta, questo test comporta una penalità aggiuntiva principalmente a causa della tecnica di assegnazione delle variabili utilizzata qui, con il risultato che la parte di assegnazione delle variabili nel piano viene elaborata in modalità riga.

Ecco il tempo e le statistiche di I/O che ho ottenuto per questa esecuzione:

Soluzioni CLR

Sia Kamil Kosno che Adam Machanic hanno inizialmente fornito una semplice soluzione solo CLR e in seguito hanno creato una combinazione CLR+T-SQL più sofisticata. Inizierò con le soluzioni di Kamil e poi tratterò le soluzioni di Adam.

Soluzioni di Kamil Kosno

Ecco il codice CLR utilizzato nella prima soluzione di Kamil per definire una funzione chiamata GetNums_KamilKosno1:

using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsKamil1
{
    [Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName = "GetNums_KamilKosno1_Fill", TableDefinition = "n BIGINT")]
    public static IEnumerator GetNums_KamilKosno1(SqlInt64 low, SqlInt64 high)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) : new GetNumsCS(low.Value, high.Value);
    }
 
    public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }
 
    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to)
        {
            _lowrange = from;
            _current = _lowrange - 1;
            _highrange = to;
        }
 
        public bool MoveNext()
        {
            _current += 1;
            if (_current > _highrange) return false;
            else return true;
        }
 
        public object Current
        {
            get
            {
 
                return _current;
            }
        }
 
        public void Reset()
        {
            _current = _lowrange - 1;
        }
 
        long _lowrange;
        long _current;
        long _highrange;
    }
}

La funzione accetta due input chiamati basso e alto e restituisce una tabella con una colonna BIGINT chiamata n. La funzione è di tipo streaming e restituisce una riga con il numero successivo nella serie per riga richiesta dalla query chiamante. Come puoi vedere, Kamil ha scelto il metodo più formalizzato per implementare l'interfaccia IEnumerator, che prevede l'implementazione dei metodi MoveNext (fa avanzare l'enumeratore per ottenere la riga successiva), Current (ottiene la riga nella posizione corrente dell'enumeratore) e Reset (imposta l'enumeratore nella sua posizione iniziale, che è prima della prima riga).

La variabile che contiene il numero corrente nella serie è chiamata _current. Il costruttore imposta _current sul limite inferiore dell'intervallo richiesto meno 1, e lo stesso vale per il metodo Reset. Il metodo MoveNext fa avanzare _current di 1. Quindi, se _current è maggiore del limite superiore dell'intervallo richiesto, il metodo restituisce false, il che significa che non verrà chiamato di nuovo. In caso contrario, restituisce true, il che significa che verrà chiamato di nuovo. Il metodo Current restituisce naturalmente _current. Come puoi vedere, logica piuttosto elementare.

Ho chiamato il progetto di Visual Studio GetNumsKamil1 e ho usato il percorso C:\Temp\ per questo. Ecco il codice che ho usato per distribuire la funzione nel database testdb:

DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno1;
 
DROP ASSEMBLY IF EXISTS GetNumsKamil1;
GO
 
CREATE ASSEMBLY GetNumsKamil1
  FROM 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll';
GO
 
CREATE FUNCTION dbo.GetNums_KamilKosno1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1;
GO

Si noti l'uso della clausola ORDER nell'istruzione CREATE FUNCTION. La funzione emette le righe in n ordinamento, quindi quando le righe devono essere inserite nel piano in n ordinamento, in base a questa clausola SQL Server sa che può evitare un ordinamento nel piano.

Testiamo la funzione, prima con la tecnica dell'aggregato, quando l'ordine non è necessario:

SELECT MAX(n) AS mx FROM dbo.GetNums_KamilKosno1(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 1.

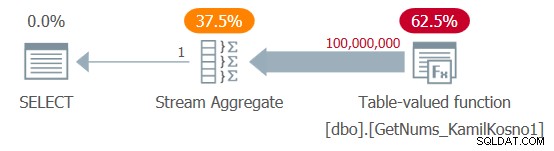Figura 1:piano per la funzione dbo.GetNums_KamilKosno1

Non c'è molto da dire su questo piano, a parte il fatto che tutti gli operatori utilizzano la modalità di esecuzione riga.

Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

E, naturalmente, non sono state coinvolte letture logiche.

Testiamo la funzione con ordine, usando la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_KamilKosno1(1, 100000000) ORDER BY n;

Ho ottenuto il piano mostrato nella Figura 2 per questa esecuzione.

Figura 2:piano per la funzione dbo.GetNums_KamilKosno1 con ORDER BY

Si noti che non c'è ordinamento nel piano poiché la funzione è stata creata con la clausola ORDER(n). Tuttavia, è necessario garantire che le righe vengano effettivamente emesse dalla funzione nell'ordine promesso. Questa operazione viene eseguita utilizzando gli operatori Segmento e Sequence Project, utilizzati per calcolare i numeri di riga, e l'operatore Assert, che interrompe l'esecuzione della query se il test non riesce. Questo lavoro ha un ridimensionamento lineare, a differenza del ridimensionamento n log n che avresti ottenuto se fosse stato richiesto un ordinamento, ma non è ancora economico. Ho le seguenti statistiche temporali per questo test:

I risultati potrebbero essere sorprendenti per alcuni, specialmente per coloro che intuitivamente presumevano che le soluzioni basate su CLR avrebbero prestazioni migliori di quelle T-SQL. Come puoi vedere, i tempi di esecuzione sono un ordine di grandezza più lunghi rispetto alla nostra soluzione T-SQL più performante.

La seconda soluzione di Kamil è un ibrido CLR-T-SQL. Oltre agli input basso e alto, la funzione CLR (GetNums_KamilKosno2) aggiunge un input di passaggio e restituisce valori compresi tra basso e alto che sono distanziati l'uno dall'altro. Ecco il codice CLR utilizzato da Kamil nella sua seconda soluzione:

using System;
using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsKamil2
{
    [Microsoft.SqlServer.Server.SqlFunction(DataAccess = Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic = true, IsPrecise = true, FillRowMethodName = "GetNums_Fill", TableDefinition = "n BIGINT")]
 
    public static IEnumerator GetNums_KamilKosno2(SqlInt64 low, SqlInt64 high, SqlInt64 step)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) : new GetNumsCS(low.Value, high.Value, step.Value);
    }
 
    public static void GetNums_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }
 
    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to, long step)
        {
            _lowrange = from;
            _step = step;
            _current = _lowrange - _step;
            _highrange = to;
        }
 
        public bool MoveNext()
        {
            _current = _current + _step;
            if (_current > _highrange) return false;
            else return true;
        }
 
        public object Current
        {
            get
            {
                return _current;
            }
        }
 
        public void Reset()
        {
            _current = _lowrange - _step;
        }
 
        long _lowrange;
        long _current;
        long _highrange;
        long _step;
    }
}

Ho chiamato il progetto VS GetNumsKamil2, l'ho inserito anche nel percorso C:\Temp\ e ho usato il codice seguente per distribuirlo nel database testdb:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno2;
DROP ASSEMBLY IF EXISTS GetNumsKamil2;
GO
 
CREATE ASSEMBLY GetNumsKamil2
  FROM 'C:\Temp\GetNumsKamil2\GetNumsKamil2\bin\Debug\GetNumsKamil2.dll';
GO
 
CREATE FUNCTION dbo.GetNums_KamilKosno2
    (@low AS BIGINT = 1, @high AS BIGINT, @step AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil2.GetNumsKamil2.GetNums_KamilKosno2;
GO

Come esempio di utilizzo della funzione, ecco una richiesta per generare valori compresi tra 5 e 59, con un passo di 10:

SELECT n FROM dbo.GetNums_KamilKosno2(5, 59, 10);

Questo codice genera il seguente output:

n
---
5
15
25
35
45
55

Per quanto riguarda la parte T-SQL, Kamil ha utilizzato una funzione chiamata dbo.GetNums_Hybrid_Kamil2, con il seguente codice:

CREATE OR ALTER FUNCTION dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@high - @low + 1) V.n
  FROM dbo.GetNums_KamilKosno2(@low, @high, 10) AS GN
    CROSS APPLY (VALUES(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n),
                       (5+GN.n),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);
GO

Come puoi vedere, la funzione T-SQL richiama la funzione CLR con gli stessi input @low e @high che ottiene e in questo esempio utilizza una dimensione del passaggio di 10. La query utilizza CROSS APPLY tra il risultato della funzione CLR e un costruttore table -value che genera i numeri finali aggiungendo valori nell'intervallo da 0 a 9 all'inizio del passaggio. Il filtro TOP viene utilizzato per assicurarti di non ricevere più del numero di numeri che hai richiesto.

Importante: Dovrei sottolineare che Kamil fa un'ipotesi qui sull'applicazione del filtro TOP in base all'ordinamento dei numeri dei risultati, che non è realmente garantito poiché la query non ha una clausola ORDER BY. Se aggiungi una clausola ORDER BY per supportare TOP, o sostituisci TOP con un filtro WHERE, per garantire un filtro deterministico, questo potrebbe cambiare completamente il profilo prestazionale della soluzione.

Ad ogni modo, testiamo prima la funzione senza ordine usando la tecnica aggregata:

SELECT MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 3 per questa esecuzione.

Figura 3:piano per la funzione dbo.GetNums_Hybrid_Kamil2

Anche in questo caso, tutti gli operatori del piano utilizzano la modalità di esecuzione riga.

Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

E naturalmente nessuna lettura logica.

Testiamo la funzione con ordine:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000) ORDER BY n;

Ho ottenuto il piano mostrato nella Figura 4.

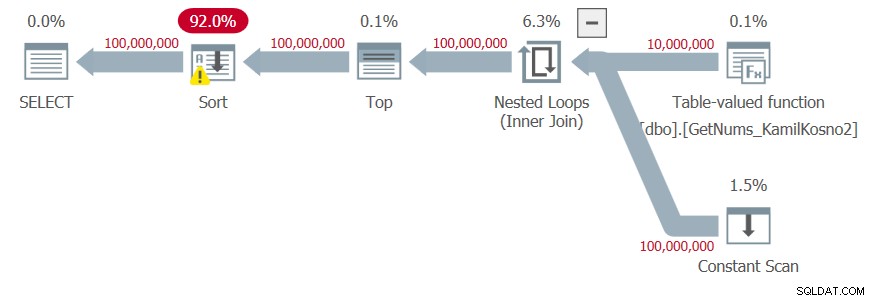Figura 4:piano per la funzione dbo.GetNums_Hybrid_Kamil2 con ORDER BY

Poiché i numeri dei risultati sono il risultato della manipolazione del limite inferiore del passaggio restituito dalla funzione CLR e del delta aggiunto nel costruttore di valori di tabella, l'ottimizzatore non si fida che i numeri dei risultati siano generati nell'ordine richiesto e aggiunge l'ordinamento esplicito al piano.

Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

Quindi sembra che quando non c'è bisogno di un ordine, la seconda soluzione di Kamil faccia meglio della prima. Ma quando è necessario l'ordine, è il contrario. Ad ogni modo, le soluzioni T-SQL sono più veloci. Personalmente mi fiderei della correttezza della prima soluzione, ma non della seconda.

Soluzioni di Adam Machanic

La prima soluzione di Adam è anche una funzione CLR di base che continua ad incrementare un contatore. Solo invece di utilizzare l'approccio formalizzato più complicato come ha fatto Kamil, Adam ha utilizzato un approccio più semplice che invoca il comando yield per riga che deve essere restituita.

Ecco il codice CLR di Adam per la sua prima soluzione, che definisce una funzione di streaming chiamata GetNums_AdamMachanic1:

using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsAdam1
{
    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic1_fill",
        TableDefinition = "n BIGINT")]
 
    public static IEnumerable GetNums_AdamMachanic1(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        for (; min_int <= max_int; min_int++)
        {
            yield return (min_int);
        }
    }
 
    public static void GetNums_AdamMachanic1_fill(object o, out long i)
    {
        i = (long)o;
    }
};

La soluzione è così elegante nella sua semplicità. Come puoi vedere, la funzione accetta due input chiamati min e max che rappresentano i punti limite inferiore e superiore dell'intervallo richiesto e restituisce una tabella con una colonna BIGINT chiamata n. La funzione inizializza le variabili denominate min_int e max_int con i valori dei parametri di input della rispettiva funzione. La funzione esegue quindi un ciclo finché min_int <=max_int, che in ogni iterazione produce una riga con il valore corrente di min_int e incrementa min_int di 1. Questo è tutto.

Ho chiamato il progetto GetNumsAdam1 in VS, l'ho inserito in C:\Temp\ e ho usato il codice seguente per distribuirlo:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic1;
DROP ASSEMBLY IF EXISTS GetNumsAdam1;
GO
 
CREATE ASSEMBLY GetNumsAdam1
  FROM 'C:\Temp\GetNumsAdam1\GetNumsAdam1\bin\Debug\GetNumsAdam1.dll';
GO
 
CREATE FUNCTION dbo.GetNums_AdamMachanic1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1;
GO

Ho usato il codice seguente per testarlo con la tecnica aggregata, per i casi in cui l'ordine non ha importanza:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic1(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 5 per questa esecuzione.

Figura 5:piano per la funzione dbo.GetNums_AdamMachanic1

Il piano è molto simile al piano che hai visto in precedenza per la prima soluzione di Kamil e lo stesso vale per le sue prestazioni. Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

E ovviamente non erano necessarie letture logiche.

Testiamo la funzione con ordine, usando la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_AdamMachanic1(1, 100000000) ORDER BY n;

Ho ottenuto il piano mostrato nella Figura 6 per questa esecuzione.

Figura 6:piano per la funzione dbo.GetNums_AdamMachanic1 con ORDER BY

Ancora una volta, il piano sembra simile a quello che hai visto prima per la prima soluzione di Kamil. Non c'era bisogno di un ordinamento esplicito poiché la funzione è stata creata con la clausola ORDER, ma il piano include del lavoro per verificare che le righe vengano effettivamente restituite ordinate come promesso.

Ho ottenuto le seguenti statistiche temporali per questa esecuzione:

Nella sua seconda soluzione, Adam ha anche combinato una parte CLR e una parte T-SQL. Ecco la descrizione di Adam della logica che ha usato nella sua soluzione:

CLR è una buona risposta per la seconda parte, ma è ovviamente ostacolato dal primo problema. Quindi, come compromesso, ho creato un TVF T-SQL [chiamato GetNums_AdamMachanic2_8192] hardcoded con i valori da 1 a 8192. (Scelta abbastanza arbitraria, ma troppo grande e il QO inizia a soffocare un po'.) Successivamente ho modificato la mia funzione CLR [ denominato GetNums_AdamMachanic2_8192_base] per generare due colonne, "max_base" e "base_add", e ha prodotto righe come:

max_base, base_add
——————
8191, 1
8192, 8192
8192, 16384
…
8192, 99991552
257, 99999744

Ora è un semplice ciclo. L'output CLR viene inviato a T-SQL TVF, che è impostato per restituire solo fino alle righe "max_base" del suo set hardcoded. E per ogni riga, aggiunge "base_add" al valore, generando così i numeri richiesti. La chiave qui, penso, è che possiamo generare N righe con un solo cross join logico e la funzione CLR deve restituire solo 1/8192 tante righe, quindi è abbastanza veloce da fungere da generatore di base.

La logica sembra piuttosto semplice.

Ecco il codice utilizzato per definire la funzione CLR denominata GetNums_AdamMachanic2_8192_base:

using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsAdam2
{
    private struct row
    {
        public long max_base;
        public long base_add;
    }
 
    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic2_8192_base_fill",
        TableDefinition = "max_base int, base_add int")]
 
    public static IEnumerable GetNums_AdamMachanic2_8192_base(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        var min_group = min_int / 8192;
        var max_group = max_int / 8192;
 
        for (; min_group <= max_group; min_group++)
        {
            if (min_int > max_int)
                yield break;
            var max_base = 8192 - (min_int % 8192);
            if (min_group == max_group && max_int < (((max_int / 8192) + 1) * 8192) - 1)
                max_base = max_int - min_int + 1;
            yield return (
                new row()
                {
                    max_base = max_base,
                    base_add = min_int
                }
            );
            min_int = (min_group + 1) * 8192;
        }
    }
 
    public static void GetNums_AdamMachanic2_8192_base_fill(object o, out long max_base, out long base_add)
    {
        var r = (row)o;
        max_base = r.max_base;
        base_add = r.base_add;
    }
};

Ho chiamato il progetto VS GetNumsAdam2 e l'ho inserito nel percorso C:\Temp\ come con gli altri progetti. Ecco il codice che ho usato per distribuire la funzione nel database testdb:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base;
DROP ASSEMBLY IF EXISTS GetNumsAdam2;
GO
 
CREATE ASSEMBLY GetNumsAdam2
  FROM 'C:\Temp\GetNumsAdam2\GetNumsAdam2\bin\Debug\GetNumsAdam2.dll';
GO
 
CREATE FUNCTION dbo.GetNums_AdamMachanic2_8192_base(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE(max_base BIGINT, base_add BIGINT)
  ORDER(base_add)
  AS EXTERNAL NAME GetNumsAdam2.GetNumsAdam2.GetNums_AdamMachanic2_8192_base;
GO

Ecco un esempio per l'utilizzo di GetNums_AdamMachanic2_8192_base con un intervallo da 1 a 100 M:

SELECT * FROM dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);

Questo codice genera il seguente output, mostrato qui in forma abbreviata:

max_base             base_add
-------------------- --------------------
8191                 1
8192                 8192
8192                 16384
8192                 24576
8192                 32768
...
8192                 99966976
8192                 99975168
8192                 99983360
8192                 99991552
257                  99999744

(12208 rows affected)

Ecco il codice con la definizione della funzione T-SQL GetNums_AdamMachanic2_8192 (abbreviata):

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@max_base) V.i + @add_base AS val
  FROM (
    VALUES
    (0),
    (1),
    (2),
    (3),
    (4),
    ...
    (8187),
    (8188),
    (8189),
    (8190),
    (8191)
  ) AS V(i);
GO

Importante: Anche qui, dovrei sottolineare che, analogamente a quanto ho detto sulla seconda soluzione di Kamil, Adam qui ipotizza che il filtro TOP estrarrà le righe superiori in base all'ordine di apparizione delle righe nel costruttore del valore della tabella, il che non è realmente garantito. Se aggiungi una clausola ORDER BY per supportare TOP o modifichi il filtro in un filtro WHERE, otterrai un filtro deterministico, ma questo può cambiare completamente il profilo delle prestazioni della soluzione.

Infine, ecco la funzione T-SQL più esterna, dbo.GetNums_AdamMachanic2, che l'utente finale chiama per ottenere la serie di numeri:

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT Y.val AS n
  FROM ( SELECT max_base, base_add
  	     FROM dbo.GetNums_AdamMachanic2_8192_base(@low, @high) ) AS X
    CROSS APPLY dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) AS Y
GO

Questa funzione utilizza l'operatore CROSS APPLY per applicare la funzione T-SQL interna dbo.GetNums_AdamMachanic2_8192 per riga restituita dalla funzione CLR interna dbo.GetNums_AdamMachanic2_8192_base.

Per prima cosa testiamo questa soluzione usando la tecnica dell'aggregato quando l'ordine non ha importanza:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic2(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 7 per questa esecuzione.

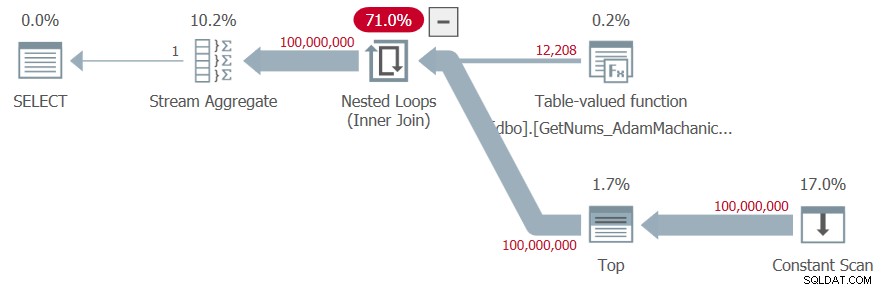Figura 7:piano per la funzione dbo.GetNums_AdamMachanic2

Ho le seguenti statistiche temporali per questo test:

Non erano necessarie letture logiche.

Il tempo di esecuzione non è male, ma si noti il ​​tempo di compilazione elevato dovuto al grande costruttore di valori di tabella utilizzato. Paghereste un tempo di compilazione così alto indipendentemente dalla dimensione dell'intervallo che richiedete, quindi questo è particolarmente complicato quando si utilizza la funzione con intervalli molto piccoli. E questa soluzione è ancora più lenta di quelle T-SQL.

Testiamo la funzione con ordine:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_AdamMachanic2(1, 100000000) ORDER BY n;

Ho ottenuto il piano mostrato nella Figura 8 per questa esecuzione.

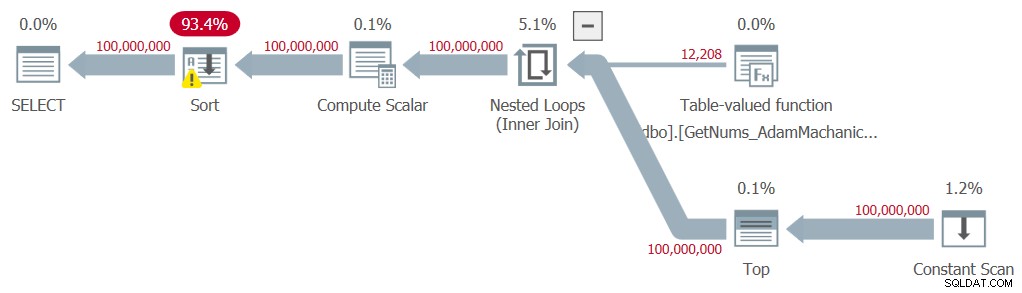Figura 8:piano per la funzione dbo.GetNums_AdamMachanic2 con ORDER BY

Come con la seconda soluzione di Kamil, nel piano è necessario un ordinamento esplicito, che prevede una significativa penalizzazione delle prestazioni. Ecco le statistiche temporali che ho ottenuto per questo test:

Inoltre, c'è ancora l'elevata penalità del tempo di compilazione di circa un terzo di secondo.

Conclusione

È stato interessante testare soluzioni basate su CLR per la sfida delle serie numeriche perché molte persone inizialmente presumevano che la soluzione con le prestazioni migliori sarebbe stata probabilmente basata su CLR. Kamil e Adam hanno utilizzato approcci simili, con il primo tentativo che utilizza un semplice ciclo che incrementa un contatore e produce una riga con il valore successivo per iterazione, e il secondo tentativo più sofisticato che combina parti CLR e T-SQL. Personalmente, non mi sento a mio agio con il fatto che sia nella seconda soluzione di Kamil che nella seconda soluzione di Adam si basassero su un filtro TOP non deterministico e quando l'ho convertito in uno deterministico nei miei test, ha avuto un impatto negativo sulle prestazioni della soluzione . In ogni caso, le nostre due soluzioni T-SQL funzionano meglio di quelle CLR e non comportano un ordinamento esplicito nel piano quando sono necessarie le righe ordinate. Quindi non vedo davvero il valore nel perseguire ulteriormente il percorso CLR. Figure 9 has a performance summary of the solutions that I presented in this article.

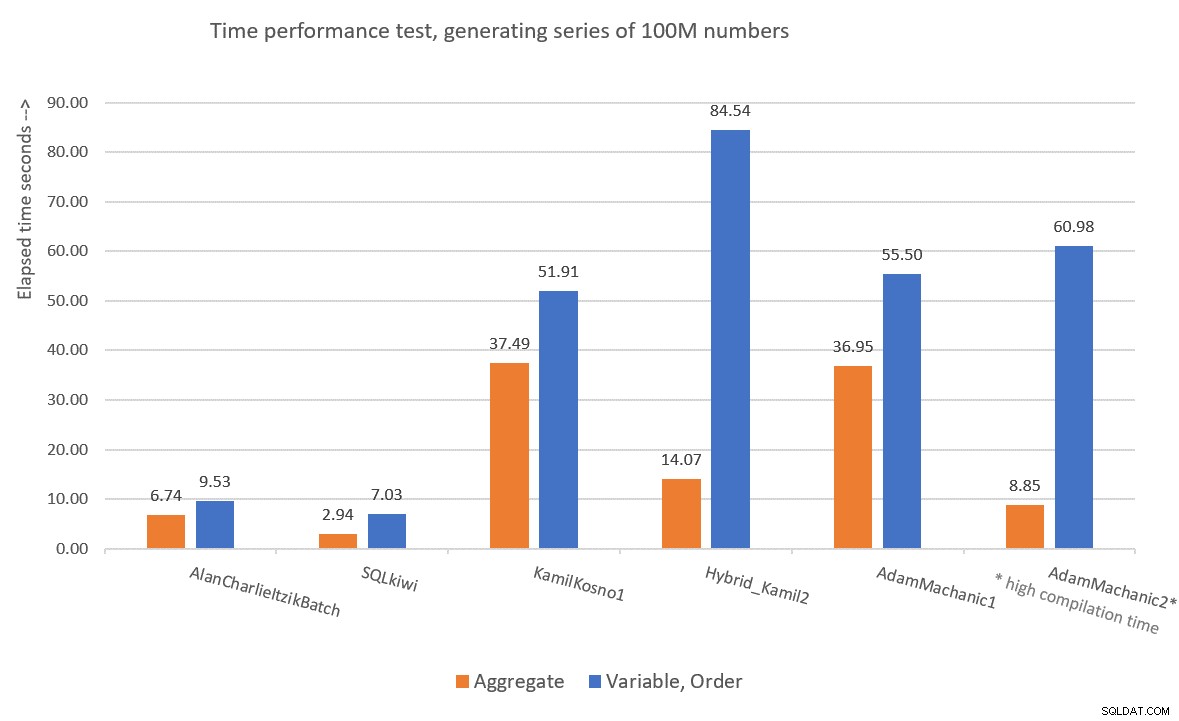Figure 9:Time performance comparison

To me, GetNums_AlanCharlieItzikBatch should be the solution of choice when you require absolutely no I/O footprint, and GetNums_SQKWiki should be preferred when you don’t mind a small I/O footprint. Of course, we can always hope that one day Microsoft will add this critically useful tool as a built-in one, and hopefully if/when they do, it will be a performant solution that supports batch processing and parallelism. So don’t forget to vote for this feature improvement request, and maybe even add your comments for why it’s important for you.

I really enjoyed working on this series. I learned a lot during the process, and hope that you did too.