Combinazioni di ritorno
Utilizzando una tabella di numeri o una CTE che genera numeri, selezionare da 0 a 2^n - 1. Utilizzando le posizioni dei bit contenenti 1 in questi numeri per indicare la presenza o l'assenza dei membri relativi nella combinazione ed eliminando quelli che non hanno il numero corretto di valori, dovresti essere in grado di restituire un set di risultati con tutte le combinazioni che desideri.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Questa query funziona abbastanza bene, ma ho pensato a un modo per ottimizzarla, sfruttando il Nifty Parallel Bit Count per ottenere prima il giusto numero di oggetti presi alla volta. Questo ha prestazioni da 3 a 3,5 volte più veloci (sia CPU che tempo):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Sono andato a leggere la pagina di conteggio dei bit e penso che questo potrebbe funzionare meglio se non faccio il % 255 ma vado fino in fondo con un po' di aritmetica. Quando ne avrò la possibilità, lo proverò e vedrò come si accumula.
Le mie dichiarazioni di prestazione si basano sulle query eseguite senza la clausola ORDER BY. Per chiarezza, ciò che sta facendo questo codice è contare il numero di 1 bit impostati in Num dai Numbers tavolo. Questo perché il numero viene utilizzato come una sorta di indicizzatore per scegliere quali elementi del set sono nella combinazione corrente, quindi il numero di 1 bit sarà lo stesso.
Spero vi piaccia!
Per la cronaca, questa tecnica di utilizzo del modello di bit di numeri interi per selezionare i membri di un set è ciò che ho coniato "Vertical Cross Join". Risulta effettivamente nel cross join di più set di dati, in cui il numero di set e cross join è arbitrario. Qui, il numero di set è il numero di elementi presi alla volta.
In realtà l'unione incrociata nel solito senso orizzontale (di aggiungere più colonne all'elenco esistente di colonne con ogni unione) sarebbe simile a questa:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Le mie query sopra "incrociate" in modo efficace tutte le volte necessarie con un solo join. I risultati sono privi di pivot rispetto ai cross join effettivi, certo, ma è una questione minore.
Critica al tuo codice
Innanzitutto, posso suggerire questa modifica alla tua UDF fattoriale:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Ora puoi calcolare insiemi di combinazioni molto più grandi, inoltre è più efficiente. Potresti anche considerare di utilizzare decimal(38, 0) per consentire calcoli intermedi più grandi nei tuoi calcoli di combinazione.
In secondo luogo, la query data non restituisce i risultati corretti. Ad esempio, utilizzando i miei dati di test dal test delle prestazioni di seguito, il set 1 è lo stesso del set 18. Sembra che la tua query prenda una striscia scorrevole che si avvolge:ogni set è sempre 5 membri adiacenti, con un aspetto simile a questo (ho ruotato per renderlo più facile da vedere):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Confronta il modello dalle mie query:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Solo per portare a casa il bit-pattern -> index of combination per chiunque sia interessato, nota che 31 in binary =11111 e il pattern è ABCDE. 121 in binario è 1111001 e il modello è A__DEFG (mappato al contrario).
Risultati delle prestazioni con una tabella di numeri reali
Ho eseguito alcuni test delle prestazioni con grandi set sulla mia seconda query sopra. Non ho un record in questo momento della versione del server utilizzata. Ecco i miei dati di prova:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter ha mostrato che questo "incrocio incrociato verticale" non funziona così come la semplice scrittura di SQL dinamico per eseguire effettivamente i CROSS JOIN che evita. Al banale costo di qualche lettura in più, la sua soluzione ha metriche tra 10 e 17 volte migliori. Le prestazioni della sua query diminuiscono più velocemente della mia all'aumentare della quantità di lavoro, ma non abbastanza da impedire a chiunque di utilizzarla.
La seconda serie di numeri di seguito è il fattore diviso per la prima riga della tabella, solo per mostrare come si ridimensiona.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Pietro
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Estrapolando, alla fine la mia query sarà più economica (sebbene sia fin dall'inizio in letture), ma non per molto tempo. Per utilizzare 21 articoli nel set è già necessaria una tabella di numeri fino a 2097152...
Ecco un commento che ho fatto inizialmente prima di rendermi conto che la mia soluzione avrebbe prestazioni nettamente migliori con una tabella numerica al volo:
Risultati delle prestazioni con una tabella dei numeri al volo
Quando inizialmente ho scritto questa risposta, ho detto:
Bene, l'ho provato e i risultati sono stati che ha funzionato molto meglio! Ecco la query che ho usato:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Nota che ho selezionato i valori in variabili per ridurre il tempo e la memoria necessari per testare tutto. Il server fa ancora lo stesso lavoro. Ho modificato la versione di Peter in modo che fosse simile e ho rimosso gli extra non necessari in modo che fossero entrambi il più snelli possibile. La versione del server utilizzata per questi test è Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) in esecuzione su una macchina virtuale.
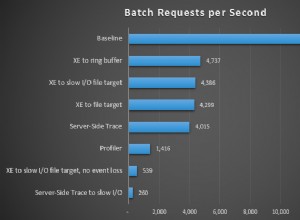
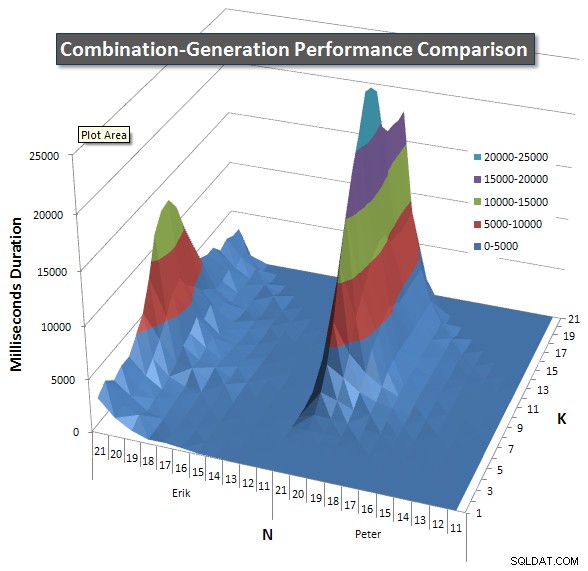
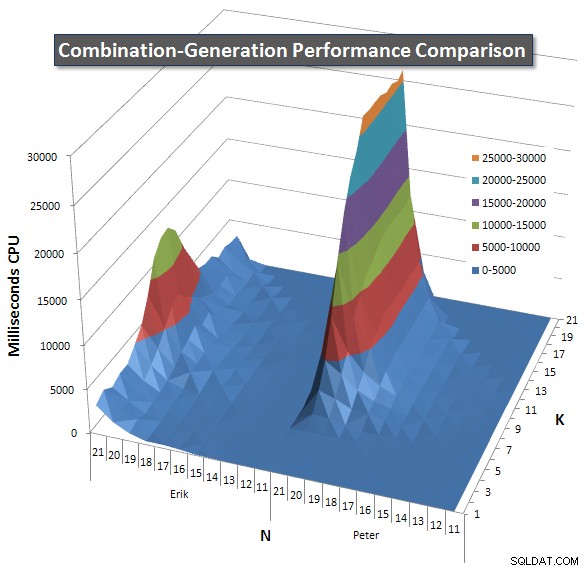
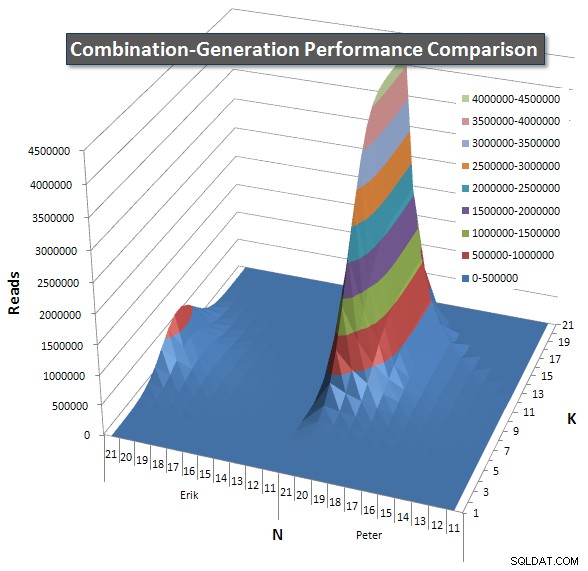
Di seguito sono riportati i grafici che mostrano le curve di prestazione per valori di N e K fino a 21. I relativi dati di base si trovano in un'altra risposta in questa pagina . I valori sono il risultato di 5 esecuzioni di ciascuna query a ciascun valore K e N, seguite dall'eliminazione dei valori migliori e peggiori per ciascuna metrica e dalla media dei restanti 3.
Fondamentalmente, la mia versione ha una "spalla" (nell'angolo più a sinistra del grafico) con valori alti di N e valori bassi di K che lo rendono peggiore rispetto alla versione SQL dinamica. Tuttavia, questo rimane abbastanza basso e costante e il picco centrale intorno a N =21 e K =11 è molto più basso per Durata, CPU e Letture rispetto alla versione SQL dinamica.
Ho incluso un grafico del numero di righe che ogni elemento dovrebbe restituire in modo da poter vedere come si comporta la query in base alla quantità di lavoro che deve svolgere.
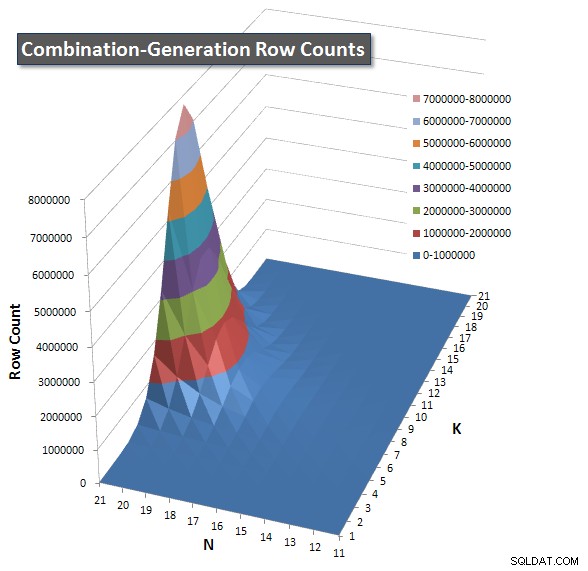
Si prega di consultare la mia risposta aggiuntiva in questa pagina per i risultati completi delle prestazioni. Ho raggiunto il limite di caratteri del post e non ho potuto includerlo qui. (Qualche idea su dove altro metterla?) Per mettere le cose in prospettiva rispetto ai risultati delle prestazioni della mia prima versione, ecco lo stesso formato di prima:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Pietro
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Conclusioni
- Le tabelle numeriche al volo sono migliori di una tabella reale contenente righe, poiché leggerne una con un numero di righe enorme richiede molto I/O. È meglio usare un po' di CPU.
- I miei test iniziali non erano abbastanza ampi per mostrare realmente le caratteristiche prestazionali delle due versioni.
- La versione di Peter potrebbe essere migliorata facendo in modo che ogni JOIN non solo sia maggiore dell'oggetto precedente, ma limiti anche il valore massimo in base a quanti altri oggetti devono essere inseriti nel set. Ad esempio, a 21 elementi presi 21 alla volta, c'è solo una risposta di 21 righe (tutti i 21 elementi, una volta), ma i set di righe intermedi nella versione SQL dinamica, all'inizio del piano di esecuzione, contengono combinazioni come " AU" al passaggio 2 anche se questo verrà scartato al prossimo join poiché non è disponibile un valore superiore a "U". Allo stesso modo, un set di righe intermedio al passaggio 5 conterrà "ARSTU" ma l'unica combinazione valida a questo punto è "ABCDE". Questa versione migliorata non avrebbe un picco più basso al centro, quindi forse non lo migliorerebbe abbastanza per diventare il chiaro vincitore, ma diventerebbe almeno simmetrico in modo che i grafici non rimangano al massimo oltre la metà della regione ma ricadano indietro vicino a 0 come fa la mia versione (vedi l'angolo superiore dei picchi per ogni query).
Analisi della durata
- Non c'è alcuna differenza davvero significativa tra le versioni in termini di durata (>100 ms) fino a 14 elementi presi 12 alla volta. Fino a questo punto, la mia versione vince 30 volte e la versione SQL dinamica vince 43 volte.
- A partire da 14•12, la mia versione era 65 volte più veloce (59>100 ms), la versione SQL dinamica 64 volte (60>100 ms). Tuttavia, tutte le volte che la mia versione era più veloce, ha risparmiato una durata media totale di 256,5 secondi e quando la versione SQL dinamica era più veloce, ha risparmiato 80,2 secondi.
- La durata media totale di tutte le prove è stata di 270,3 secondi per Erik, 446,2 secondi per Peter.
- Se viene creata una tabella di ricerca per determinare quale versione utilizzare (scegliendo quella più veloce per gli input), tutti i risultati potrebbero essere eseguiti in 188,7 secondi. L'utilizzo di quello più lento ogni volta richiederebbe 527,7 secondi.
Legge l'analisi
L'analisi della durata ha mostrato che la mia query ha vinto per un importo significativo ma non eccessivamente grande. Quando la metrica passa alle letture, emerge un'immagine molto diversa:la mia query utilizza in media 1/10 delle letture.
- Non c'è alcuna differenza davvero significativa tra le versioni in letture (>1000) fino a 9 elementi presi 9 alla volta. Fino a questo punto, la mia versione vince 30 volte e la versione SQL dinamica vince 17 volte.
- A partire da 9•9, la mia versione ha utilizzato meno letture 118 volte (113>1000), la versione SQL dinamica 69 volte (31>1000). Tuttavia, tutte le volte che la mia versione ha utilizzato meno letture, ha salvato una media totale di 75,9 milioni di letture e quando la versione SQL dinamica era più veloce, ha salvato 380.000 letture.
- La media totale delle letture per tutte le prove è stata di 8,4 milioni di Erik, 84 milioni di Peter.
- Se viene creata una tabella di ricerca per determinare quale versione utilizzare (scegliendo quella migliore per gli input), tutti i risultati potrebbero essere eseguiti in 8 milioni di letture. L'utilizzo del peggiore ogni volta richiederebbe 84,3 milioni di letture.
Sarei molto interessato a vedere i risultati di una versione SQL dinamica aggiornata che pone il limite superiore aggiuntivo sugli elementi scelti ad ogni passaggio come ho descritto sopra.
Addendum
La versione seguente della mia query ottiene un miglioramento di circa il 2,25% rispetto ai risultati delle prestazioni sopra elencati. Ho usato il metodo di conteggio dei bit HAKMEM del MIT e ho aggiunto un Convert(int) sul risultato di row_number() poiché restituisce un bigint. Ovviamente vorrei che questa fosse la versione con cui avevo usato per tutti i test delle prestazioni, i grafici e i dati di cui sopra, ma è improbabile che la rifarò mai perché era laboriosa.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
E non ho potuto resistere a mostrare un'altra versione che esegue una ricerca per ottenere il conteggio dei bit. Potrebbe anche essere più veloce di altre versioni:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))