Soluzioni per la sfida del generatore di serie numeriche - Parte 4

Questa è la quarta parte di una serie sulle soluzioni alla sfida del generatore di serie numeriche. Mille grazie ad Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea e Paul White per aver condiviso idee e commenti.

Amo il lavoro di Paul White. Continuo a essere scioccato dalle sue scoperte e mi chiedo come diavolo fa a capire cosa fa. Mi piace anche il suo stile di scrittura efficiente ed eloquente. Spesso, mentre leggo i suoi articoli o post, scuoto la testa e dico a mia moglie, Lilach, che da grande voglio essere proprio come Paul.

Quando ho inizialmente pubblicato la sfida, speravo segretamente che Paul pubblicasse una soluzione. Sapevo che se l'avesse fatto, sarebbe stato molto speciale. Bene, lo ha fatto, ed è affascinante! Ha prestazioni eccellenti e c'è molto da imparare da esso. Questo articolo è dedicato alla soluzione di Paul.

Farò i miei test in tempdb, abilitando I/O e statistiche temporali:

SET NOCOUNT ON;
 
USE tempdb;
 
SET STATISTICS TIME, IO ON;

Limitazioni delle idee precedenti

Valutando le soluzioni precedenti, uno dei fattori importanti per ottenere buone prestazioni era la capacità di utilizzare l'elaborazione batch. Ma l'abbiamo sfruttato al massimo?

Esaminiamo i piani per due delle soluzioni precedenti che utilizzavano l'elaborazione batch. Nella parte 1 ho trattato la funzione dbo.GetNumsAlanCharlieItzikBatch, che combinava le idee di Alan, Charlie e me stesso.

Ecco la definizione della funzione:

-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
 
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
 
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Questa soluzione definisce un costruttore di valori di tabella di base con 16 righe e una serie di CTE a cascata con join incrociati per aumentare il numero di righe potenzialmente a 4B. La soluzione utilizza la funzione ROW_NUMBER per creare la sequenza di base dei numeri in un CTE chiamato Nums e il filtro TOP per filtrare la cardinalità della serie numerica desiderata. Per abilitare l'elaborazione batch, la soluzione utilizza un join sinistro fittizio con una condizione falsa tra Nums CTE e una tabella denominata dbo.BatchMe, che ha un indice columnstore.

Utilizzare il codice seguente per testare la funzione con la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

La rappresentazione di Plan Explorer dell'effettivo il piano per questa esecuzione è mostrato nella Figura 1.

Figura 1:piano per la funzione dbo.GetNumsAlanCharlieItzikBatch

Quando si analizza l'elaborazione in modalità batch rispetto alla modalità riga, è abbastanza bello poter dire semplicemente guardando un piano ad alto livello quale modalità di elaborazione utilizzata da ciascun operatore. In effetti, Plan Explorer mostra una figura batch azzurra nella parte in basso a sinistra dell'operatore quando la sua modalità di esecuzione effettiva è Batch. Come puoi vedere nella Figura 1, l'unico operatore che ha utilizzato la modalità batch è l'operatore Window Aggregate, che calcola i numeri di riga. C'è ancora molto lavoro svolto da altri operatori in modalità riga.

Ecco i numeri delle prestazioni che ho ottenuto nel mio test:

letture logiche 0

Per identificare quali operatori hanno impiegato più tempo per l'esecuzione, utilizzare l'opzione Piano di esecuzione effettivo in SSMS o l'opzione Ottieni piano effettivo in Plan Explorer. Assicurati di leggere il recente articolo di Paul Capire i tempi dell'operatore del piano di esecuzione. L'articolo descrive come normalizzare i tempi di esecuzione degli operatori riportati per ottenere i numeri corretti.

Nel piano in Figura 1, la maggior parte del tempo viene trascorsa dagli operatori Nested Loop e Top più a sinistra, entrambi in esecuzione in modalità riga. Oltre a essere meno efficiente della modalità batch per le operazioni a uso intensivo della CPU, tieni presente che il passaggio dalla modalità riga alla modalità batch e viceversa comporta costi aggiuntivi.

Nella parte 2 ho trattato un'altra soluzione che utilizzava l'elaborazione batch, implementata nella funzione dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Questa soluzione combinava le idee di John Number2, Dave Mason, Joe Obbish, Alan, Charlie e me. La differenza principale tra la soluzione precedente e questa è che come unità di base, la prima utilizza un costruttore di valori di tabella virtuale e la seconda utilizza una tabella reale con un indice columnstore, offrendo l'elaborazione batch "gratuitamente". Ecco il codice che crea la tabella e la popola utilizzando un'istruzione INSERT con 102.400 righe per ottenere la compressione:

DROP TABLE IF EXISTS dbo.NullBits102400;
GO
 
CREATE TABLE dbo.NullBits102400
(
  b BIT NULL, 
  INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
    WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
 
WITH
  L0 AS (SELECT CAST(NULL AS BIT) AS b
         FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
  L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
  nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b) 
  SELECT TOP(102400) b FROM nulls;
GO

Ecco la definizione della funzione:

CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
  (@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
  WITH
    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
             FROM dbo.NullBits102400 AS A
               CROSS JOIN dbo.NullBits102400 AS B)
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

Un singolo cross join tra due istanze della tabella di base è sufficiente per produrre ben oltre il potenziale desiderato di 4B righe. Anche in questo caso, la soluzione utilizza la funzione ROW_NUMBER per produrre la sequenza di base dei numeri e il filtro TOP per limitare la cardinalità della serie di numeri desiderata.

Ecco il codice per testare la funzione utilizzando la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Il piano per questa esecuzione è mostrato nella Figura 2.

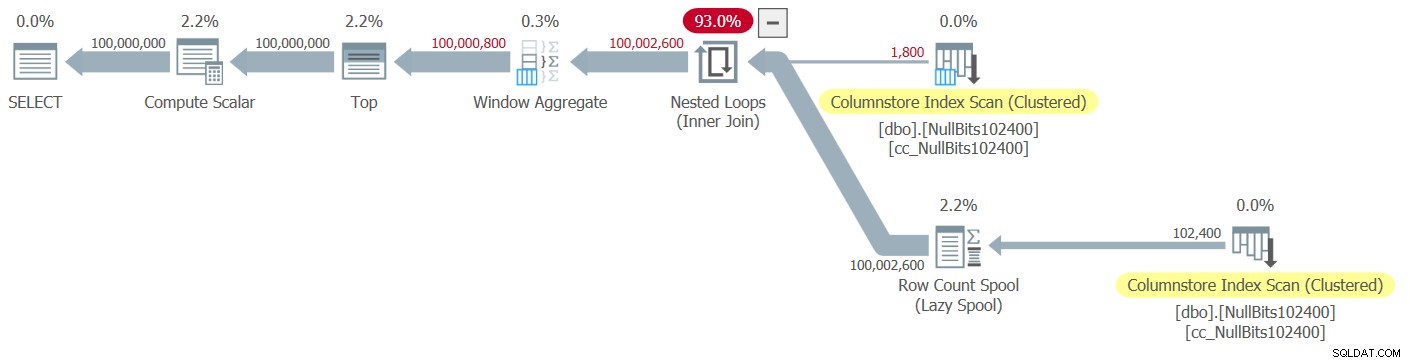Figura 2:piano per la funzione dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2

Osserva che solo due operatori in questo piano utilizzano la modalità batch:la scansione superiore dell'indice columnstore cluster della tabella, che viene utilizzato come input esterno del join Nested Loops, e l'operatore Window Aggregate, che viene utilizzato per calcolare i numeri di riga di base .

Ho ottenuto i seguenti numeri di prestazioni per il mio test:

Tabella 'NullBits102400'. Conteggio scansioni 2, letture logiche 0, letture fisiche 0, letture del page server 0, letture read-ahead 0, letture read-ahead del server delle pagine 0, letture logiche lob 8, letture fisiche lob 0, letture del server delle pagine lob 0, letture lob- avanti legge 0, il server di pagina lob read-ahead legge 0.

Tabella 'NullBits102400'. Il segmento legge 2, il segmento è saltato 0.

Anche in questo caso, la maggior parte del tempo nell'esecuzione di questo piano viene speso dagli operatori Nested Loop e Top più a sinistra, che vengono eseguiti in modalità riga.

La soluzione di Paolo

Prima di presentare la soluzione di Paul, inizierò con la mia teoria sul processo di pensiero che ha attraversato. Questo è in realtà un ottimo esercizio di apprendimento e ti suggerisco di affrontarlo prima di cercare la soluzione. Paul ha riconosciuto gli effetti debilitanti di un piano che mescola sia modalità batch che modalità riga e si è proposto una sfida per trovare una soluzione che ottenga un piano in modalità batch. In caso di successo, il potenziale per una tale soluzione di funzionare bene è piuttosto alto. È certamente intrigante vedere se un tale obiettivo è raggiungibile dato che ci sono ancora molti operatori che non supportano ancora la modalità batch e molti fattori che inibiscono l'elaborazione batch. Ad esempio, al momento della scrittura, l'unico algoritmo di join che supporta l'elaborazione batch è l'algoritmo di hash join. Un cross join viene ottimizzato utilizzando l'algoritmo dei cicli annidati. Inoltre, l'operatore Top è attualmente implementato solo in modalità riga. Questi due elementi sono elementi fondamentali critici utilizzati nei piani per molte delle soluzioni che ho trattato finora, comprese le due precedenti.

Supponendo che tu abbia dato una prova decente alla sfida di creare una soluzione con un piano in modalità batch, passiamo al secondo esercizio. Per prima cosa presenterò la soluzione di Paul così come l'ha fornita, con i suoi commenti in linea. Lo eseguirò anche per confrontare le sue prestazioni con le altre soluzioni. Ho imparato molto decostruendo e ricostruendo la sua soluzione, un passo alla volta, per assicurarmi di aver capito attentamente perché ha usato ciascuna delle tecniche che ha fatto. Ti suggerisco di fare lo stesso prima di passare a leggere le mie spiegazioni.

Ecco la soluzione di Paul, che prevede una tabella columnstore helper chiamata dbo.CS e una funzione chiamata dbo.GetNums_SQLkiwi:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
        @low - 2 + N.rn < @high;
GO

Ecco il codice che ho usato per testare la funzione con la tecnica di assegnazione delle variabili:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 3 per il mio test.

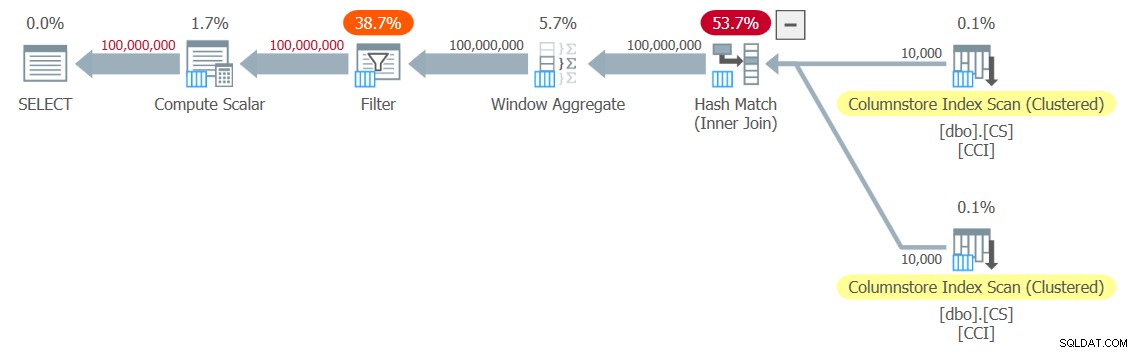Figura 3:piano per la funzione dbo.GetNums_SQLkiwi

È un piano in modalità batch! È abbastanza impressionante.

Ecco i numeri delle prestazioni che ho ottenuto per questo test sulla mia macchina:

Tabella 'CS'. Conteggio scansioni 2, letture logiche 0, letture fisiche 0, letture del page server 0, letture read-ahead 0, letture read-ahead del server delle pagine 0, letture logiche lob 44, letture fisiche lob 0, letture del server delle pagine lob 0, letture lob- avanti legge 0, il server di pagina lob read-ahead legge 0.

Tabella 'CS'. Il segmento legge 2, il segmento è saltato 0.

Verifichiamo anche che se è necessario restituire i numeri ordinati per n, la soluzione è la conservazione dell'ordine rispetto a rn, almeno quando si utilizzano costanti come input, ed evitare quindi l'ordinamento esplicito nel piano. Ecco il codice per testarlo con ordine:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;

Ottieni lo stesso piano della Figura 3, e quindi numeri di prestazioni simili:

Tabella 'CS'. Conteggio scansioni 2, letture logiche 0, letture fisiche 0, letture del page server 0, letture read-ahead 0, letture read-ahead del server delle pagine 0, letture logiche lob 44, letture fisiche lob 0, letture del server delle pagine lob 0, letture lob- avanti legge 0, il server di pagina lob read-ahead legge 0.

Tabella 'CS'. Il segmento legge 2, il segmento è saltato 0.

Questo è un aspetto importante della soluzione.

Cambiare la nostra metodologia di test

Le prestazioni della soluzione di Paul sono un discreto miglioramento sia del tempo trascorso che del tempo della CPU rispetto alle due soluzioni precedenti, ma non sembra il miglioramento più drammatico che ci si aspetterebbe da un piano in modalità batch. Forse ci sfugge qualcosa?

Proviamo ad analizzare i tempi di esecuzione dell'operatore osservando il piano di esecuzione effettivo in SSMS come mostrato nella Figura 4.

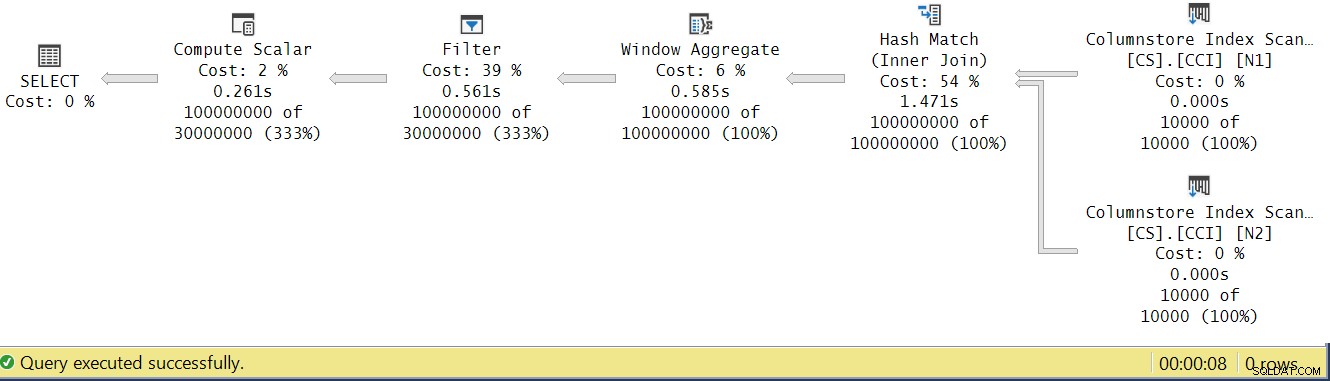Figura 4:Tempi di esecuzione dell'operatore per la funzione dbo.GetNums_SQLkiwi

Nell'articolo di Paul sull'analisi dei tempi di esecuzione degli operatori, spiega che con gli operatori in modalità batch ciascuno riporta il proprio tempo di esecuzione. Se sommi i tempi di esecuzione di tutti gli operatori in questo piano effettivo, otterrai 2,878 secondi, ma il piano ha impiegato 7,876 per essere eseguito. Sembrano mancare 5 secondi del tempo di esecuzione. La risposta a questo sta nella tecnica di test che stiamo usando, con l'assegnazione delle variabili. Ricordiamo che abbiamo deciso di utilizzare questa tecnica per eliminare la necessità di inviare tutte le righe dal server al chiamante ed evitare gli I/O che sarebbero coinvolti nella scrittura del risultato in una tabella. Sembrava l'opzione perfetta. Tuttavia, il vero costo dell'assegnazione delle variabili è nascosto in questo piano e, naturalmente, viene eseguito in modalità riga. Mistero risolto.

Ovviamente in fin dei conti un buon test è un test che riflette adeguatamente il vostro uso produttivo della soluzione. Se in genere scrivi i dati su una tabella, è necessario che il test lo rifletta. Se invii il risultato al chiamante, è necessario che il tuo test lo rifletta. Ad ogni modo, l'assegnazione delle variabili sembra rappresentare una parte importante del tempo di esecuzione nel nostro test, ed è chiaramente improbabile che rappresenti un uso tipico di produzione della funzione. Paul ha suggerito che invece dell'assegnazione di variabili il test potrebbe applicare un semplice aggregato come MAX alla colonna del numero restituito (n/rn/op). Un operatore aggregato può utilizzare l'elaborazione batch, quindi il piano non comporterebbe la conversione dalla modalità batch alla modalità riga come risultato del suo utilizzo e il suo contributo al tempo di esecuzione totale dovrebbe essere abbastanza piccolo e noto.

Quindi testiamo nuovamente tutte e tre le soluzioni trattate in questo articolo. Ecco il codice per testare la funzione dbo.GetNumsAlanCharlieItzikBatch:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Ho ottenuto il piano mostrato nella Figura 5 per questo test.

Figura 5:piano per la funzione dbo.GetNumsAlanCharlieItzikBatch con aggregato

Ecco i numeri delle prestazioni che ho ottenuto per questo test:

letture logiche 0

Osservare che il tempo di esecuzione è sceso da 10,025 secondi utilizzando la tecnica di assegnazione variabile a 8,733 utilizzando la tecnica aggregata. È poco più di un secondo di tempo di esecuzione che possiamo attribuire all'assegnazione della variabile qui.

Ecco il codice per testare la funzione dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2:

SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Ho ottenuto il piano mostrato nella Figura 6 per questo test.

Figura 6:piano per la funzione dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 con aggregate

Ecco i numeri delle prestazioni che ho ottenuto per questo test:

Tabella 'NullBits102400'. Conteggio scansioni 2, letture logiche 0, letture fisiche 0, letture del page server 0, letture read-ahead 0, letture read-ahead del server delle pagine 0, letture logiche lob 8, letture fisiche lob 0, letture del server delle pagine lob 0, letture lob- avanti legge 0, il server di pagina lob read-ahead legge 0.

Tabella 'NullBits102400'. Il segmento legge 2, il segmento è saltato 0.

Osservare che il tempo di esecuzione è sceso da 9,813 secondi utilizzando la tecnica di assegnazione variabile a 7,053 utilizzando la tecnica aggregata. Sono poco più di due secondi di tempo di esecuzione che possiamo attribuire all'assegnazione della variabile qui.

Ed ecco il codice per testare la soluzione di Paul:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Ottengo il piano mostrato nella Figura 7 per questo test.

Figura 7:piano per la funzione dbo.GetNums_SQLkiwi con aggregato

E ora per il grande momento. Ho ottenuto i seguenti numeri di prestazioni per questo test:

Tabella 'CS'. Conteggio scansioni 2, letture logiche 0, letture fisiche 0, letture del page server 0, letture read-ahead 0, letture read-ahead del server delle pagine 0, letture logiche lob 44, letture fisiche lob 0, letture del server delle pagine lob 0, letture lob- avanti legge 0, il server di pagina lob read-ahead legge 0.

Tabella 'CS'. Il segmento legge 2, il segmento è saltato 0.

Il tempo di esecuzione è sceso da 7.822 secondi a 3.149 secondi! Esaminiamo i tempi di esecuzione dell'operatore nel piano effettivo in SSMS, come mostrato nella Figura 8.

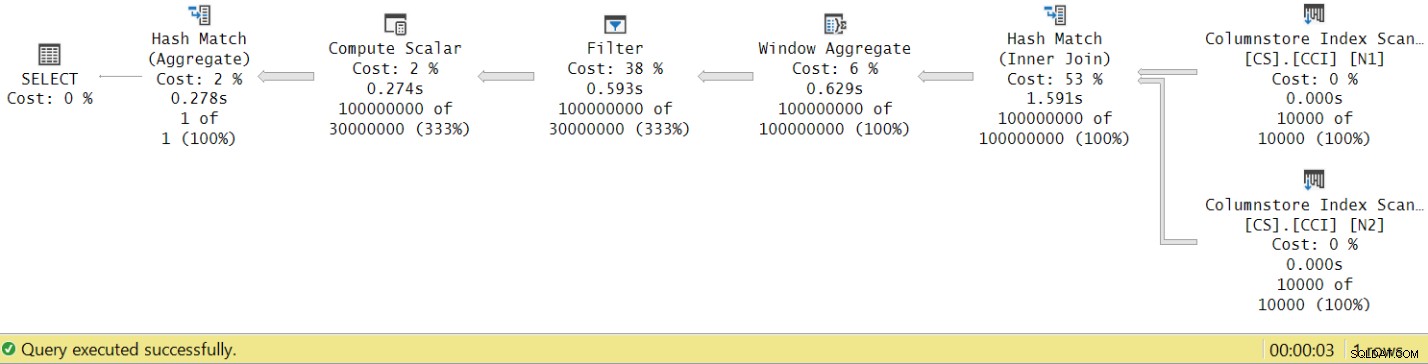Figura 8:Tempi di esecuzione dell'operatore per la funzione dbo.GetNums con aggregate

Ora se accumuli i tempi di esecuzione dei singoli operatori otterrai un numero simile al tempo totale di esecuzione del piano.

La Figura 9 mostra un confronto delle prestazioni in termini di tempo trascorso tra le tre soluzioni utilizzando sia l'assegnazione variabile che le tecniche di test aggregato.

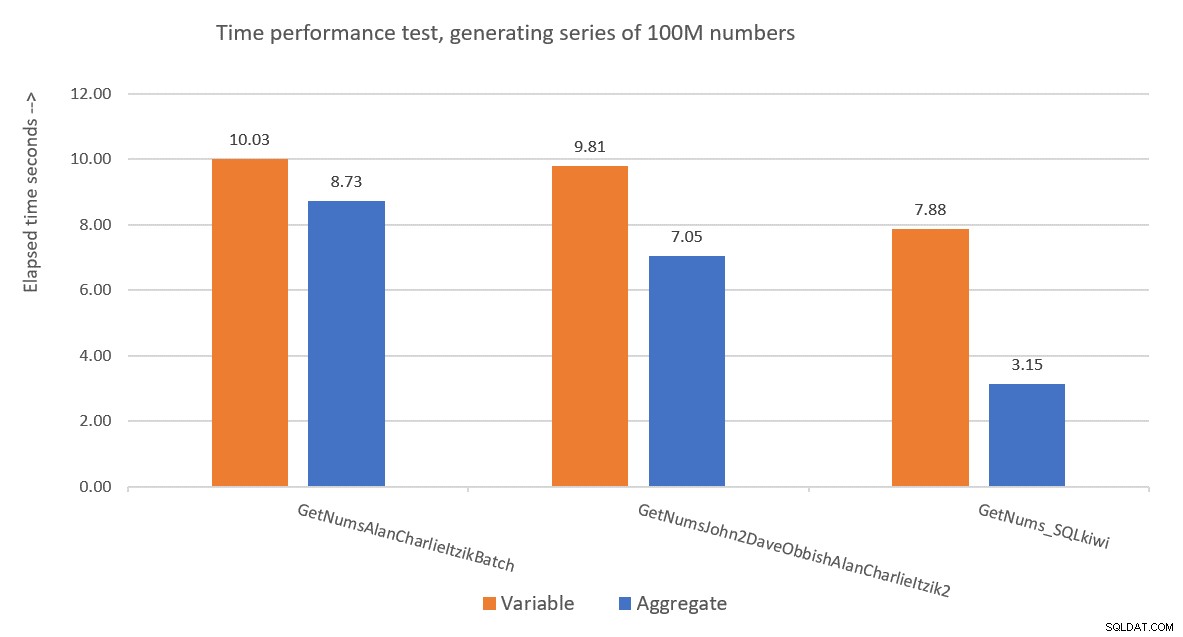Figura 9:confronto delle prestazioni

La soluzione di Paul è un chiaro vincitore, e questo è particolarmente evidente quando si utilizza la tecnica del test aggregato. Che impresa impressionante!

Decostruzione e ricostruzione della soluzione di Paolo

Decostruire e poi ricostruire la soluzione di Paul è un ottimo esercizio e impari molto mentre lo fai. Come suggerito in precedenza, ti consiglio di eseguire tu stesso il processo prima di continuare a leggere.

La prima scelta che devi fare è la tecnica che useresti per generare il numero potenziale desiderato di righe di 4B. Paul ha scelto di utilizzare una tabella columnstore e di popolarla con tante righe quante sono la radice quadrata del numero richiesto, ovvero 65.536 righe, in modo che con un unico cross join si otterrebbe il numero richiesto. Forse stai pensando che con meno di 102.400 righe non otterresti un gruppo di righe compresso, ma questo si applica quando si popola la tabella con un'istruzione INSERT come abbiamo fatto con la tabella dbo.NullBits102400. Non si applica quando crei un indice columnstore su una tabella prepopolata. Quindi Paul ha utilizzato un'istruzione SELECT INTO per creare e popolare la tabella come un heap basato su rowstore con 65.536 righe, quindi ha creato un indice columnstore cluster, risultando in un gruppo di righe compresso.

La prossima sfida è capire come ottenere un cross join da elaborare con un operatore in modalità batch. Per questo, è necessario che l'algoritmo di join sia hash. Ricorda che un cross join viene ottimizzato utilizzando l'algoritmo dei cicli annidati. In qualche modo devi indurre l'ottimizzatore a pensare che stai usando un equijoin interno (l'hash richiede almeno un predicato basato sull'uguaglianza), ma in pratica ottieni un cross join.

Un primo tentativo ovvio consiste nell'usare un inner join con un predicato di join artificiale che sia sempre vero, in questo modo:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON 0 = 0;

Ma questo codice non riesce con il seguente errore:

L'ottimizzatore di SQL Server riconosce che si tratta di un predicato di inner join artificiale, semplifica l'inner join in un cross join e genera un errore in cui si dice che non può accogliere il suggerimento per forzare un algoritmo di hash join.

Per risolvere questo problema, Paul ha creato una colonna INT NOT NULL (più sul perché questa specifica a breve) chiamata n1 nella sua tabella dbo.CS e l'ha popolata con 0 in tutte le righe. Ha quindi utilizzato il predicato join N2.n1 =N1.n1, ottenendo effettivamente la proposizione 0 =0 in tutte le valutazioni di corrispondenza, rispettando i requisiti minimi per un algoritmo di hash join.

Funziona e produce un piano in modalità batch:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON N2.n1 = N1.n1;

Quanto al motivo per cui n1 deve essere definito come INT NOT NULL; perché non consentire NULL e perché non usare BIGINT? Il motivo di queste scelte è evitare un residuo di hash probe (un filtro aggiuntivo applicato dall'operatore di hash join oltre il predicato di join originale), che potrebbe comportare costi aggiuntivi non necessari. Per i dettagli, vedere l'articolo di Paul Unisci prestazioni, conversioni implicite e residui. Ecco la parte dell'articolo che ci interessa:

Tieni presente che questa ottimizzazione non si applica alle colonne bigint."

Per verificare questo aspetto, creiamo un'altra tabella chiamata dbo.CS2 con una colonna n1 nullable:

DROP TABLE IF EXISTS dbo.CS2;
 
SELECT * INTO dbo.CS2 FROM dbo.CS;
 
ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL;
 
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS2
WITH (MAXDOP = 1);

Per prima cosa testiamo una query su dbo.CS (dove n1 è definito come INT NOT NULL), generando 4B numeri di riga di base in una colonna chiamata rn e applicando l'aggregato MAX alla colonna:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    JOIN dbo.CS AS N2
        ON N2.n1 = N1.n1
) AS N;

Confronteremo il piano per questa query con il piano per una query simile rispetto a dbo.CS2 (dove n1 è definito come INT NULL):

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS2 AS N1
    JOIN dbo.CS2 AS N2
        ON N2.n1 = N1.n1
) AS N;

I piani per entrambe le query sono mostrati nella Figura 10.

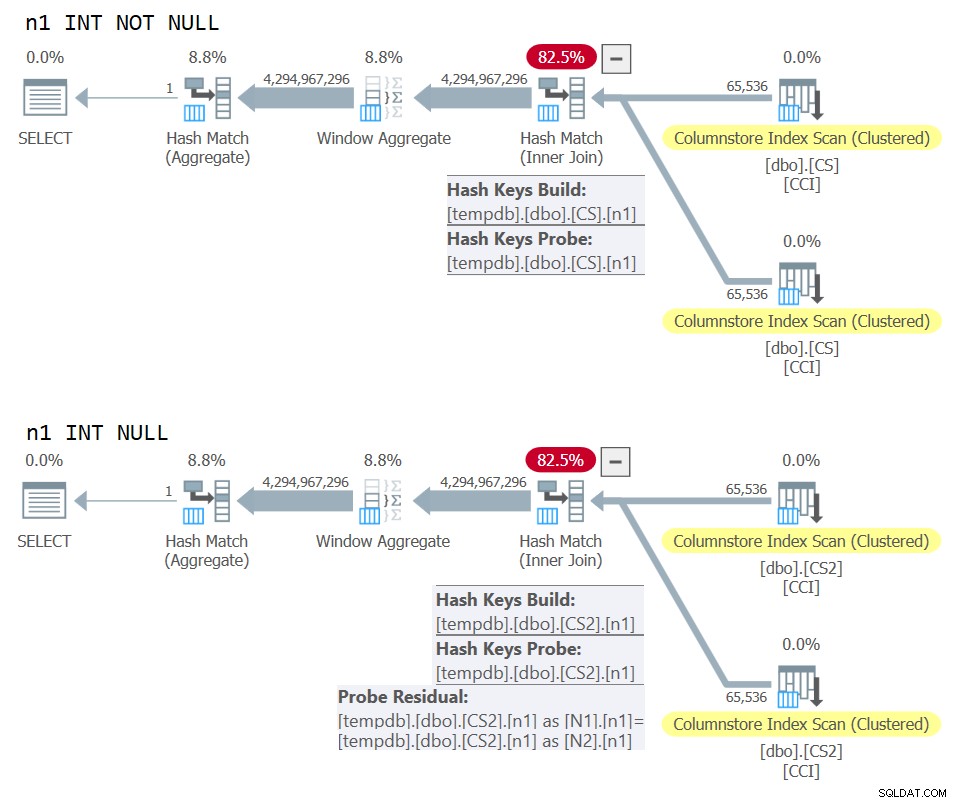Figura 10:confronto del piano per la chiave di unione NOT NULL e NULL

Puoi vedere chiaramente il residuo sonda extra applicato nel secondo piano ma non nel primo.

Sulla mia macchina la query contro dbo.CS è stata completata in 91 secondi e la query contro dbo.CS2 è stata completata in 92 secondi. Nell'articolo di Paul riporta una differenza dell'11% a favore del caso NOT NULL per l'esempio che ha utilizzato.

A proposito, quelli di voi con un occhio attento avranno notato l'uso di ORDER BY @@TRANCOUNT come specifica di ordinazione della funzione ROW_NUMBER. Se leggi attentamente i commenti in linea di Paul nella sua soluzione, afferma che l'uso della funzione @@TRANCOUNT è un inibitore del parallelismo, mentre l'uso di @@SPID non lo è. Quindi puoi utilizzare @@TRANCOUNT come costante del tempo di esecuzione nelle specifiche di ordinazione quando vuoi forzare un piano seriale e @@SPID quando non lo fai.

Come accennato, la query su dbo.CS ha impiegato 91 secondi per essere eseguita sulla mia macchina. A questo punto potrebbe essere interessante testare lo stesso codice con un vero cross join, lasciando che l'ottimizzatore utilizzi un algoritmo di join di loop annidato in modalità riga:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    CROSS JOIN dbo.CS AS N2
) AS N;

Ci sono voluti questo codice 104 secondi per completare sulla mia macchina. Quindi otteniamo un notevole miglioramento delle prestazioni con l'hash join in modalità batch.

Il nostro prossimo problema è il fatto che quando si utilizza TOP per filtrare il numero di righe desiderato, si ottiene un piano con un operatore Top in modalità riga. Ecco un tentativo di implementare la funzione dbo.GetNums_SQLkiwi con un filtro TOP:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT TOP (100000000 - 1 + 1)
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        ORDER BY rn
    ) AS N;
GO

Proviamo la funzione:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 11 per questo test.

Figura 11:piano con filtro TOP

Osserva che l'operatore Top è l'unico nel piano che utilizza l'elaborazione in modalità riga.

Ho le seguenti statistiche temporali per questa esecuzione:

La maggior parte del tempo di esecuzione in questo piano viene spesa dall'operatore Top in modalità riga e dal fatto che il piano deve passare attraverso la conversione da batch a modalità riga e viceversa.

La nostra sfida è trovare un'alternativa di filtraggio in modalità batch al TOP in modalità riga. I filtri basati sui predicati come quelli applicati con la clausola WHERE possono essere potenzialmente gestiti con l'elaborazione batch.

L'approccio di Paul è stato quello di introdurre una seconda colonna di tipo INT (vedi il commento in linea "tutto è normalizzato a 64 bit comunque in modalità columnstore/batch" ) ha chiamato n2 nella tabella dbo.CS e la popola con la sequenza di interi da 1 a 65.536. Nel codice della soluzione ha utilizzato due filtri basati sui predicati. Uno è un filtro grossolano nella query interna con predicati che coinvolgono la colonna n2 da entrambi i lati del join. Questo filtro grossolano può causare alcuni falsi positivi. Ecco il primo tentativo semplicistico di un filtro del genere:

WHERE
    -- Coarse filter:
    N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

Con gli ingressi 1 e 100.000.000 come @basso e @alto, non ottieni falsi positivi. Ma prova con 1 e 100.000.001 e ne ottieni alcuni. Otterrai una sequenza di 100.020.001 numeri invece di 100.000.001.

Per eliminare i falsi positivi, Paul ha aggiunto un secondo filtro preciso che coinvolge la colonna rn nella query esterna. Ecco il primo tentativo semplicistico di un filtro così preciso:

WHERE
    -- Precise filter:
    N.rn < @high - @low + 2

Rivediamo la definizione della funzione per utilizzare i filtri basati sui predicati sopra invece di TOP, prendiamo 1:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        N.rn < @high - @low + 2;
GO

Proviamo la funzione:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ho ottenuto il piano mostrato nella Figura 12 per questo test.

Figura 12:piano con filtro WHERE, prendi 1

Ahimè, qualcosa è chiaramente andato storto. SQL Server ha convertito il nostro filtro basato sui predicati che coinvolge la colonna rn in un filtro basato su TOP e lo ha ottimizzato con un operatore Top, che è esattamente ciò che abbiamo cercato di evitare. Per aggiungere la beffa al danno, l'ottimizzatore ha anche deciso di utilizzare l'algoritmo dei cicli annidati per il join.

Ci sono voluti questo codice 18,8 secondi per finire sulla mia macchina. Non ha un bell'aspetto.

Per quanto riguarda il join dei loop nidificati, questo è qualcosa di cui potremmo facilmente occuparci usando un suggerimento di join nella query interna. Solo per vedere l'impatto sulle prestazioni, ecco un test con un suggerimento per la query hash join forzato utilizzato nella query di test stessa:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);

Il tempo di esecuzione si riduce a 13,2 secondi.

Abbiamo ancora il problema con la conversione del filtro WHERE contro rn in un filtro TOP. Proviamo a capire come è successo. Abbiamo utilizzato il seguente filtro nella query esterna:

WHERE N.rn < @high - @low + 2

Ricorda che rn rappresenta un'espressione basata su ROW_NUMBER non manipolata. Un filtro basato su un'espressione così non manipolata che si trova in un determinato intervallo è spesso ottimizzato con un operatore Top, il che per noi è una cattiva notizia a causa dell'uso dell'elaborazione in modalità riga.

La soluzione alternativa di Paul consisteva nell'usare un predicato equivalente, ma che applicasse la manipolazione a rn, in questo modo:

WHERE @low - 2 + N.rn < @high

Il filtraggio di un'espressione che aggiunge la manipolazione a un'espressione basata su ROW_NUMBER inibisce la conversione del filtro basato sul predicato in uno basato su TOP. Fantastico!

Rivediamo la definizione della funzione per utilizzare il predicato WHERE sopra, prendi 2:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        @low - 2 + N.rn < @high;
GO

Testare di nuovo la funzione, senza alcun suggerimento speciale o altro:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

Ottiene naturalmente un piano in modalità batch con un algoritmo di hash join e nessun operatore Top, con un tempo di esecuzione di 3,177 secondi. Bello.

Il passaggio successivo consiste nel verificare se la soluzione gestisce bene gli input errati. Proviamo con un delta negativo:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

Questa esecuzione non riesce con il seguente errore.

La soluzione di Paul prevedeva due aggiunte. Uno consiste nell'aggiungere il seguente predicato alla clausola WHERE della query interna:

 @high >= @low

Questo filtro fa più di quello che sembra inizialmente. Se hai letto attentamente i commenti in linea di Paul, potresti trovare questa parte:

The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.

The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high>=@low.

Before the IIF addition, for example, the predicate involving N1.n2 looked like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

After adding IIF, it looks like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))

With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:

WHERE
    1 >= 100000000
    AND ...

The whole plan can then be simplified to a single Constant Scan operator. Try it:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

The plan for this execution is shown in Figure 13.

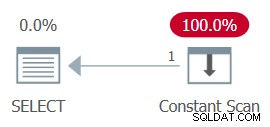Figure 13:Plan with constant scan

Unsurprisingly, I got the following performance numbers for this execution:

logical reads 0

When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.

Now let’s test the function with a valid input range:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

You get the all-batch-mode plan shown in Figure 14.

Figure 14:Plan for dbo.GetNums_SQLkiwi function

This is the same plan you saw earlier in Figure 7.

I got the following time statistics for this execution:

Ladies and gentlemen, I think we have a winner! :)

Conclusione

I’ll have what Paul’s having.

Are we done yet, or is this series going to last forever?

No and no.