Una parte importante dell'ottimizzazione delle query è la comprensione degli algoritmi disponibili per l'ottimizzatore per gestire vari costrutti di query, ad esempio filtraggio, unione, raggruppamento e aggregazione e come si ridimensionano. Questa conoscenza ti aiuta a preparare un ambiente fisico ottimale per le tue query, come la creazione degli indici giusti. Ti aiuta anche a percepire intuitivamente quale algoritmo dovresti aspettarti di vedere nel piano in un determinato insieme di circostanze, in base alla tua familiarità con le soglie in cui l'ottimizzatore dovrebbe passare da un algoritmo all'altro. Quindi, durante l'ottimizzazione delle query con prestazioni scadenti, puoi individuare più facilmente le aree nel piano delle query in cui l'ottimizzatore potrebbe aver effettuato scelte non ottimali, ad esempio a causa di stime di cardinalità imprecise, e agire per risolverle.
Un'altra parte importante dell'ottimizzazione delle query è pensare fuori dagli schemi, al di là degli algoritmi disponibili per l'ottimizzatore quando si utilizzano gli strumenti ovvi. Essere creativo. Supponiamo che tu abbia una query che funziona male anche se hai organizzato l'ambiente fisico ottimale. Per i costrutti di query utilizzati, gli algoritmi disponibili per l'ottimizzatore sono x, yez e l'ottimizzatore ha scelto il meglio che poteva in quelle circostanze. Tuttavia, la query funziona male. Riuscite a immaginare un piano teorico con un algoritmo in grado di produrre una query con prestazioni molto migliori? Se riesci a immaginarlo, è probabile che sarai in grado di ottenerlo con qualche riscrittura di query, magari con costrutti di query meno ovvi per l'attività.
In questa serie di articoli, mi concentro sul raggruppamento e sull'aggregazione dei dati. Inizierò esaminando gli algoritmi disponibili per l'ottimizzatore quando si utilizzano query raggruppate. Descriverò quindi scenari in cui nessuno degli algoritmi esistenti funziona bene e mostrerò le riscritture delle query che si traducono in prestazioni e ridimensionamento eccellenti.
Vorrei ringraziare Craig Freedman, Vassilis Papadimos e Joe Sack, membri dell'incrocio tra l'insieme delle persone più intelligenti del pianeta e l'insieme degli sviluppatori di SQL Server, per aver risposto alle mie domande sull'ottimizzazione delle query!
Per i dati di esempio userò un database chiamato PerformanceV3. È possibile scaricare uno script per creare e popolare il database da qui. Userò una tabella chiamata dbo.Orders, che è popolata con 1.000.000 di righe. Questa tabella ha un paio di indici che non sono necessari e potrebbero interferire con i miei esempi, quindi esegui il codice seguente per eliminare quegli indici non necessari:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Gli unici due indici rimasti in questa tabella sono un indice cluster chiamato idx_cl_od nella colonna orderdate e un indice univoco non cluster chiamato PK_Orders nella colonna orderid, che applica il vincolo della chiave primaria.
EXEC sys.sp_helpindex 'dbo.Orders';
index_name index_description index_keys ----------- ----------------------------------------------------- ----------- idx_cl_od clustered located on PRIMARY orderdate PK_Orders nonclustered, unique, primary key located on PRIMARY orderid
Algoritmi esistenti
SQL Server supporta due algoritmi principali per l'aggregazione dei dati:Stream Aggregate e Hash Aggregate. Con le query raggruppate, l'algoritmo Stream Aggregate richiede che i dati siano ordinati in base alle colonne raggruppate, quindi è necessario distinguere tra due casi. Uno è uno Stream Aggregate preordinato, ad esempio, quando i dati vengono ottenuti preordinati da un indice. Un altro è uno Stream Aggregate non preordinato, in cui è necessario un passaggio aggiuntivo per ordinare in modo esplicito l'input. Questi due casi si ridimensionano in modo molto diverso, quindi potresti anche considerarli come due algoritmi diversi.
L'algoritmo Hash Aggregate organizza i gruppi e i loro aggregati in una tabella hash. Non richiede l'input da ordinare.
Con dati sufficienti, l'ottimizzatore considera la parallelizzazione del lavoro, applicando ciò che è noto come aggregato locale-globale. In tal caso, l'input viene suddiviso in più thread e ciascun thread applica uno dei suddetti algoritmi per aggregare localmente il proprio sottoinsieme di righe. Un aggregato globale utilizza quindi uno dei suddetti algoritmi per aggregare i risultati degli aggregati locali.
In questo articolo mi concentro sull'algoritmo Stream Aggregate preordinato e sul suo ridimensionamento. Nelle parti future di questa serie tratterò altri algoritmi e descriverò le soglie in cui l'ottimizzatore passa dall'uno all'altro e quando dovresti considerare la riscrittura delle query.
Aggregato stream preordinato
Data una query raggruppata con un insieme di raggruppamento non vuoto (l'insieme di espressioni in base al quale si raggruppa), l'algoritmo Stream Aggregate richiede che le righe di input siano ordinate in base alle espressioni che formano l'insieme di raggruppamento. Quando l'algoritmo elabora la prima riga di un gruppo, inizializza un membro che detiene il valore aggregato intermedio con il valore pertinente (ad esempio, il valore della prima riga per un aggregato MAX). Quando elabora una riga non prima del gruppo, assegna a quel membro il risultato di un calcolo che coinvolge il valore aggregato intermedio e il valore della nuova riga (ad esempio, il massimo tra il valore aggregato intermedio e il nuovo valore). Non appena uno qualsiasi dei membri del gruppo di raggruppamento cambia il proprio valore o l'input viene consumato, il valore aggregato corrente viene considerato il risultato finale per l'ultimo gruppo.
Un modo per avere i dati ordinati come ha bisogno l'algoritmo Stream Aggregate è ottenerli preordinati da un indice. È necessario definire l'indice con le colonne del gruppo di raggruppamento come chiavi, in qualsiasi ordine tra di esse. Vuoi anche che l'indice copra. Ad esempio, considera la seguente query (la chiameremo Query 1):
SELECT shipperid, MAX(orderdate) AS maxorderid FROM dbo.Orders GROUP BY shipperid;
Un indice rowstore ottimale per supportare questa query sarebbe quello definito con shipperid come colonna chiave iniziale e orderdate come colonna inclusa o come seconda colonna chiave:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate);
Con questo indice attivo, ottieni il piano stimato mostrato nella Figura 1 (usando SentryOne Plan Explorer).

Figura 1:piano per la query 1
Si noti che l'operatore Index Scan ha una proprietà Ordered:True che indica che è necessario fornire le righe ordinate dalla chiave di indice. L'operatore Stream Aggregate quindi inserisce le righe ordinate come necessario. Quanto a come viene calcolato il costo dell'operatore; prima di arrivare a questo, prima una breve prefazione...
Come forse già saprai, quando SQL Server ottimizza una query, valuta più piani candidati e, infine, seleziona quello con il costo stimato più basso. Il costo del piano stimato è la somma di tutti i costi stimati degli operatori. A sua volta, il costo stimato di ciascun operatore è la somma del costo di I/O stimato e del costo stimato della CPU. L'unità di costo è di per sé priva di significato. La sua rilevanza è nel confronto che l'ottimizzatore fa tra i piani candidati. Cioè, le formule di costo sono state progettate con l'obiettivo che, tra i piani candidati, quello con il costo più basso rappresenti (si spera) quello che finirà più rapidamente. Un compito terribilmente complesso da svolgere con precisione!
Più le formule di determinazione dei costi tengono adeguatamente conto dei fattori che influenzano realmente le prestazioni e il ridimensionamento dell'algoritmo, più sono accurati e più è probabile che, date stime accurate della cardinalità, l'ottimizzatore scelga il piano ottimale. In ogni caso, se vuoi capire perché l'ottimizzatore sceglie un algoritmo rispetto a un altro, devi capire due cose principali:una è il modo in cui gli algoritmi funzionano e si adattano e un'altra è il modello di costo di SQL Server.
Quindi torniamo al piano in Figura 1; proviamo a capire come si calcolano i costi. Come criterio, Microsoft non rivelerà le formule dei costi interni che utilizzano. Da bambino ero affascinato dall'idea di smontare le cose. Orologi, radio, cassette (sì, sono così vecchio), lo chiami. Volevo sapere come erano fatte le cose. Allo stesso modo, vedo valore nel reverse engineering delle formule poiché se riesco a prevedere il costo in modo ragionevolmente accurato, probabilmente significa che capisco bene l'algoritmo. Durante il processo impari molto.
La nostra query acquisisce 1.000.000 di righe. Anche con questo numero di righe, il costo di I/O sembra essere trascurabile rispetto al costo della CPU, quindi è probabilmente sicuro ignorarlo.
Per quanto riguarda il costo della CPU, vuoi provare a capire quali fattori lo influenzano e in che modo. Teoricamente potrebbero esserci una serie di fattori:numero di righe di input, numero di gruppi, cardinalità dell'insieme di raggruppamento, tipo di dati e dimensione dei membri dell'insieme di raggruppamento. Pertanto, per provare a misurare l'effetto di uno qualsiasi di questi fattori, si desidera confrontare i costi stimati di due query che differiscono solo per il fattore che si desidera misurare. Ad esempio, per misurare l'impatto del numero di righe sul costo, avere due query con un numero diverso di righe di input, ma con tutti gli altri aspetti uguali (numero di gruppi, cardinalità dell'insieme di raggruppamento, ecc.). Inoltre, è importante verificare che i numeri stimati, non quelli effettivi, siano quelli desiderati poiché l'ottimizzatore si basa sui numeri stimati per calcolare i costi.
Quando si eseguono tali confronti, è bene disporre di tecniche che consentono di controllare completamente i numeri stimati. Ad esempio, un modo semplice per controllare il numero stimato di righe di input consiste nell'interrogare un'espressione di tabella basata su una query TOP e applicare la funzione di aggregazione nella query esterna. Se temi che, a causa dell'utilizzo dell'operatore TOP, l'ottimizzatore applichi obiettivi di riga e che questi si traducano in un adeguamento dei costi originali, ciò si applica solo agli operatori che appaiono nel piano sotto l'operatore Top (al a destra), non sopra (a sinistra). L'operatore Stream Aggregate appare naturalmente sopra l'operatore Principale nel piano poiché inserisce le righe filtrate.
Per quanto riguarda il controllo del numero stimato di gruppi di output, è possibile farlo utilizzando l'espressione di raggruppamento
Per assicurarti di ottenere l'algoritmo Stream Aggregate e un piano seriale puoi forzarlo con i suggerimenti per la query:OPTION(ORDER GROUP, MAXDOP 1).
Vuoi anche capire se c'è un costo di avvio per l'operatore in modo da poterlo tenere in considerazione nella tua formula di reverse engineering.
Iniziamo con il capire in che modo il numero di righe di input influisce sul costo stimato della CPU dell'operatore. Chiaramente, questo fattore dovrebbe essere rilevante per il costo dell'operatore. Inoltre, ti aspetteresti che il costo per riga sia costante. Ecco un paio di query per il confronto che differiscono solo per il numero stimato di righe di input (chiamatele rispettivamente Query 2 e Query 3):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La figura 2 contiene le parti rilevanti dei piani stimati per queste query:

Figura 2:Piani per Query 2 e Query 3
Supponendo che il costo per riga sia costante, puoi calcolarlo come la differenza tra i costi dell'operatore diviso per la differenza tra le cardinalità di input dell'operatore:
CPU cost per row = (0.125 - 0.065) / (200000 - 100000) = 0.0000006
Per verificare che il numero ottenuto sia effettivamente costante e corretto, puoi provare a prevedere i costi stimati nelle query con altri numeri di righe di input. Ad esempio, il costo previsto con 500.000 righe di input è:
Cost for 500K input rows = <cost for 100K input rows> + 400000 * 0.0000006 = 0.065 + 0.24 = 0.305
Utilizza la seguente query per verificare se la tua previsione è accurata (chiamala Query 4):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La parte rilevante del piano per questa query è mostrata nella Figura 3.
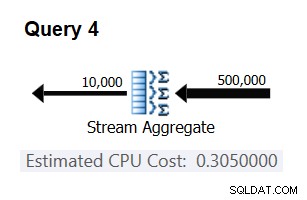
Figura 3:piano per la query 4
Bingo. Naturalmente, è una buona idea controllare più cardinalità di input aggiuntive. Con tutti quelli che ho controllato, la tesi che esiste un costo costante per riga di input di 0,0000006 era corretta.
Quindi, proviamo a capire in che modo il numero stimato di gruppi influisce sul costo della CPU dell'operatore. Ti aspetteresti che sia necessario un po' di lavoro sulla CPU per elaborare ciascun gruppo, ed è anche ragionevole aspettarsi che sia costante per gruppo. Per testare questa tesi e calcolare il costo per gruppo, puoi utilizzare le due query seguenti, che differiscono solo per il numero di gruppi di risultati (chiamateli rispettivamente Query 5 e Query 6):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 20000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 20000 OPTION(ORDER GROUP, MAXDOP 1);
Le parti rilevanti dei piani di query stimati sono mostrate nella Figura 4.
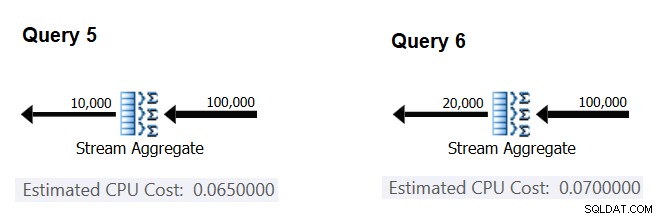
Figura 4:Piani per Query 5 e Query 6
In modo simile al modo in cui hai calcolato il costo fisso per riga di input, puoi calcolare il costo fisso per gruppo di output come la differenza tra i costi dell'operatore divisa per la differenza tra le cardinalità di output dell'operatore:
CPU cost per group = (0.07 - 0.065) / (20000 - 10000) = 0.0000005
E proprio come ho dimostrato prima, puoi verificare i tuoi risultati prevedendo i costi con altri numeri di gruppi di output e confrontando i tuoi numeri previsti con quelli prodotti dall'ottimizzatore. Con tutti i numeri di gruppi che ho provato, i costi previsti erano accurati.
Utilizzando tecniche simili, puoi verificare se altri fattori influiscono sul costo dell'operatore. I miei test mostrano che la cardinalità dell'insieme di raggruppamento (numero di espressioni raggruppate), i tipi di dati e le dimensioni delle espressioni raggruppate non hanno alcun impatto sul costo stimato.
Ciò che resta da fare è verificare se è previsto un costo di avvio significativo per l'operatore. Se ce n'è una, la formula completa (si spera) per calcolare il costo della CPU dell'operatore dovrebbe essere:
Operator CPU cost = <startup cost> + <#input rows> * 0.0000006 + <#output groups> * 0.0000005
Quindi puoi ricavare il costo di avvio dal resto:
Startup cost =- (<#input rows> * 0.0000006 + <#output groups> * 0.0000005)
È possibile utilizzare qualsiasi piano di query di questo articolo per questo scopo. Ad esempio, utilizzando i numeri del piano per la query 5 mostrati in precedenza nella figura 4, si ottiene:
Startup cost = 0.065 - (100000 * 0.0000006 + 10000 * 0.0000005) = 0
Come sembrerebbe, l'operatore Stream Aggregate non ha alcun costo di avvio relativo alla CPU, oppure è così basso da non essere mostrato con la precisione della misura dei costi.
In conclusione, la formula di reverse engineering per il costo dell'operatore Stream Aggregate è:
I/O cost: negligible CPU cost: <#input rows> * 0.0000006 + <#output groups> * 0.0000005
La figura 5 mostra il ridimensionamento del costo dell'operatore Stream Aggregate rispetto sia al numero di righe che al numero di gruppi.
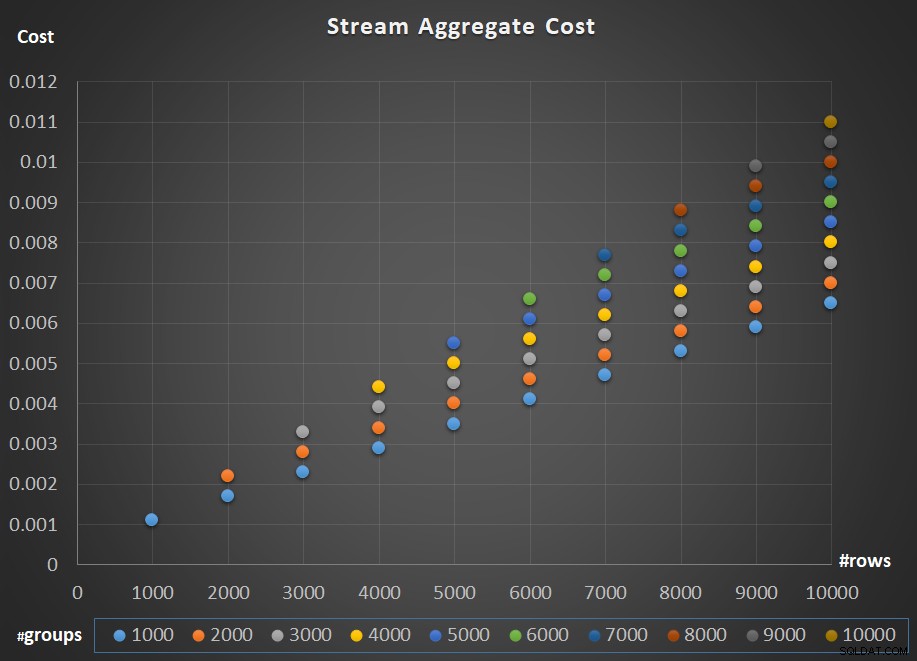
Figura 5:grafico di ridimensionamento dell'algoritmo Stream Aggregate
Per quanto riguarda il ridimensionamento dell'operatore; è lineare. Nei casi in cui il numero di gruppi tende ad essere proporzionale al numero di file, il costo dell'intero operatore aumenta dello stesso fattore che aumenta sia il numero di file che i gruppi. Ciò significa che il raddoppio del numero di righe di input e gruppi di input comporta il raddoppio del costo dell'intero operatore. Per capire perché, supponiamo di rappresentare il costo dell'operatore come:
r * 0.0000006 + g * 0.0000005
Se aumenti sia il numero di righe che il numero di gruppi dello stesso fattore p, ottieni:
pr * 0.0000006 + pg * 0.0000005 = p * (r * 0.0000006 + g * 0.0000005)
Quindi se, per un dato numero di righe e gruppi, il costo dell'operatore Stream Aggregate è C, aumentando sia il numero di righe che di gruppi dello stesso fattore p si ottiene un costo operatore di pC. Vedi se riesci a verificarlo identificando esempi nel grafico in Figura 5.
Nei casi in cui il numero di gruppi rimane abbastanza stabile anche quando il numero di righe di input aumenta, si ottiene comunque un ridimensionamento lineare. Consideri solo il costo associato al numero di gruppi come una costante. Ovvero se per un dato numero di righe e gruppi il costo dell'operatore è C =G (costo associato al numero di gruppi) più R (costo associato al numero di righe), aumentando solo il numero di righe di un fattore di p risulta in G + pR. In tal caso, naturalmente, il costo dell'intero operatore è inferiore a pC. Cioè, raddoppiando il numero di righe si ottiene meno del raddoppio del costo dell'intero operatore.
In pratica, in molti casi quando si raggruppano i dati, il numero di righe di input è sostanzialmente maggiore del numero di gruppi di output. Questo fatto, unito al fatto che il costo allocato per riga e il costo per gruppo sono pressoché uguali, la quota del costo dell'operatore attribuita al numero dei gruppi diventa trascurabile. Ad esempio, vedere il piano per la query 1 mostrato in precedenza nella Figura 1. In questi casi, è lecito pensare al costo dell'operatore semplicemente come ridimensionamento lineare rispetto al numero di righe di input.
Casi speciali
Ci sono casi speciali in cui l'operatore Stream Aggregate non ha bisogno che i dati siano ordinati. Se ci pensi, l'algoritmo Stream Aggregate ha un requisito di ordinamento più rilassato dall'input rispetto a quando hai bisogno dei dati ordinati per scopi di presentazione, ad esempio, quando la query ha una presentazione ORDER BY di presentazione esterna. L'algoritmo Stream Aggregate richiede semplicemente che tutte le righe dello stesso gruppo siano ordinate insieme. Prendi il set di input {5, 1, 5, 2, 1, 2}. Ai fini dell'ordinamento della presentazione, questo set deve essere ordinato in questo modo:1, 1, 2, 2, 5, 5. Ai fini dell'aggregazione, l'algoritmo Stream Aggregate funzionerebbe comunque bene se i dati fossero disposti nel seguente ordine:5, 5, 1, 1, 2, 2. Tenendo presente questo, quando si calcola un aggregato scalare (interrogazione con una funzione di aggregazione e senza clausola GROUP BY) o si raggruppano i dati in base a un insieme di raggruppamento vuoto, non c'è mai più di un gruppo . Indipendentemente dall'ordine delle righe di input, è possibile applicare l'algoritmo Stream Aggregate. L'algoritmo Hash Aggregate esegue l'hashing dei dati in base alle espressioni dell'insieme di raggruppamento come input, e sia con aggregati scalari che con un insieme di raggruppamento vuoto, non ci sono input da cui eseguire l'hashing. Pertanto, sia con aggregati scalari che con aggregati applicati a un insieme di raggruppamento vuoto, l'ottimizzatore utilizza sempre l'algoritmo Stream Aggregate, senza richiedere il preordine dei dati. Questo è almeno il caso in modalità di esecuzione di riga, poiché attualmente (a partire da SQL Server 2017 CU4) la modalità batch è disponibile solo con l'algoritmo Hash Aggregate. Userò le seguenti due query per dimostrarlo (chiamatele Query 7 e Query 8):
SELECT COUNT(*) AS numrows FROM dbo.Orders; SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY ();
I piani per queste query sono mostrati nella Figura 6.
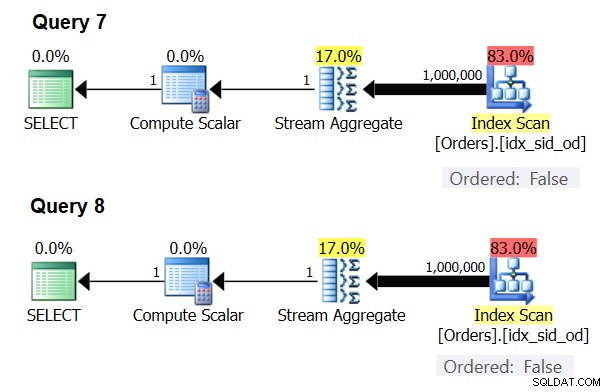
Figura 6:Piani per Query 7 e Query 8
Prova a forzare un algoritmo Hash Aggregate in entrambi i casi:
SELECT COUNT(*) AS numrows FROM dbo.Orders OPTION(HASH GROUP); SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY () OPTION(HASH GROUP);
L'ottimizzatore ignora la tua richiesta e produce gli stessi piani mostrati nella Figura 6.
Quiz rapido:qual è la differenza tra un aggregato scalare e un aggregato applicato a un insieme di raggruppamento vuoto?
Risposta:con un set di input vuoto, un aggregato scalare restituisce un risultato con una riga, mentre un aggregato in una query con un set di raggruppamento vuoto restituisce un set di risultati vuoto. Provalo:
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2;
numrows ----------- 0 (1 row affected)
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2 GROUP BY ();
numrows ----------- (0 rows affected)
Al termine, esegui il codice seguente per la pulizia:
DROP INDEX idx_sid_od ON dbo.Orders;
Riepilogo e sfida
Il reverse engineering della formula dei costi per l'algoritmo Stream Aggregate è un gioco da ragazzi. Avrei potuto solo dirti che la formula di costo per un algoritmo Stream Aggregate preordinato è @numrows * 0.0000006 + @numgroups * 0.0000005 invece di un intero articolo per spiegare come capirlo. Il punto, tuttavia, era descrivere il processo ei principi del reverse engineering, prima di passare agli algoritmi più complessi e alle soglie in cui un algoritmo diventa più ottimale degli altri. Insegnarti a pescare invece di darti un tipo di pesce. Ho imparato così tanto e ho scoperto cose a cui non avevo nemmeno pensato, mentre cercavo di decodificare le formule dei costi per vari algoritmi.
Pronto a mettere alla prova le tue abilità? La tua missione, se dovessi scegliere di accettarla, è molto più difficile del reverse engineering dell'operatore Stream Aggregate. Eseguire il reverse engineering della formula di determinazione dei costi di un operatore di ordinamento seriale. Questo è importante per la nostra ricerca poiché un algoritmo Stream Aggregate applicato per una query con un insieme di raggruppamento non vuoto, in cui i dati di input non sono preordinati, richiede un ordinamento esplicito. In tal caso, il costo e il ridimensionamento dell'operazione aggregata dipendono dal costo e dal ridimensionamento degli operatori Sort e Stream Aggregate combinati.
Se riesci ad avvicinarti decentemente alla previsione del costo dell'operatore di smistamento, puoi sentirti come se ti fossi guadagnato il diritto di aggiungere alla tua firma "Reverse Engineer". Ci sono molti ingegneri del software là fuori; ma di certo non vedi molti ingegneri inversi! Assicurati solo di testare la tua formula sia con numeri piccoli che con numeri grandi; potresti essere sorpreso da ciò che trovi.