Database
 sql >> Database >  >> RDS >> Database

Abbinare domanda e offerta:soluzioni, parte 2

[ Vai a:Sfida originale | Soluzioni:Parte 1 | Parte 2 | parte 3]

In questo articolo, continuo la copertura delle soluzioni alla sfida allettante di corrispondenza tra domanda e offerta di Peter Larsson. Grazie ancora a Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie e Peter Larsson, per aver inviato le vostre soluzioni.

Il mese scorso ho trattato una soluzione basata sulle intersezioni di intervallo, utilizzando un classico test di intersezione di intervallo basato su predicati. Chiamerò quella soluzione intersezioni classiche . L'approccio classico delle intersezioni di intervallo risulta in un piano con scala quadratica (N^2). Ho dimostrato le sue scarse prestazioni rispetto a input di esempio che vanno da 100.000 a 400.000 righe. Ci sono voluti 931 secondi per completare la soluzione rispetto all'input di 400.000 righe! Questo mese inizierò ricordandoti brevemente la soluzione del mese scorso e perché si adatta e funziona così male. Introdurrò quindi un approccio basato su una revisione del test di intersezione dell'intervallo. Questo approccio è stato utilizzato da Luca, Kamil e forse anche Daniel e consente una soluzione con prestazioni e ridimensionamento molto migliori. Chiamerò quella soluzione intersezioni riviste .

Il problema con il test di intersezione classico

Iniziamo con un rapido promemoria della soluzione del mese scorso.

Ho utilizzato i seguenti indici nella tabella dbo.Auctions di input per supportare il calcolo dei totali parziali che producono gli intervalli di domanda e offerta:

-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

Il codice seguente ha la soluzione completa che implementa il classico approccio alle intersezioni di intervallo:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Questo codice inizia calcolando gli intervalli di domanda e offerta e scrivendoli in tabelle temporanee denominate #Demand e #Supply. Il codice crea quindi un indice cluster su #Supply con EndSupply come chiave principale per supportare il test di intersezione nel miglior modo possibile. Infine, il codice unisce #Supply e #Demand, identificando gli scambi come i segmenti sovrapposti degli intervalli di intersezione, utilizzando il seguente predicato di join basato sul classico test di intersezione degli intervalli:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

Il piano per questa soluzione è mostrato nella Figura 1.

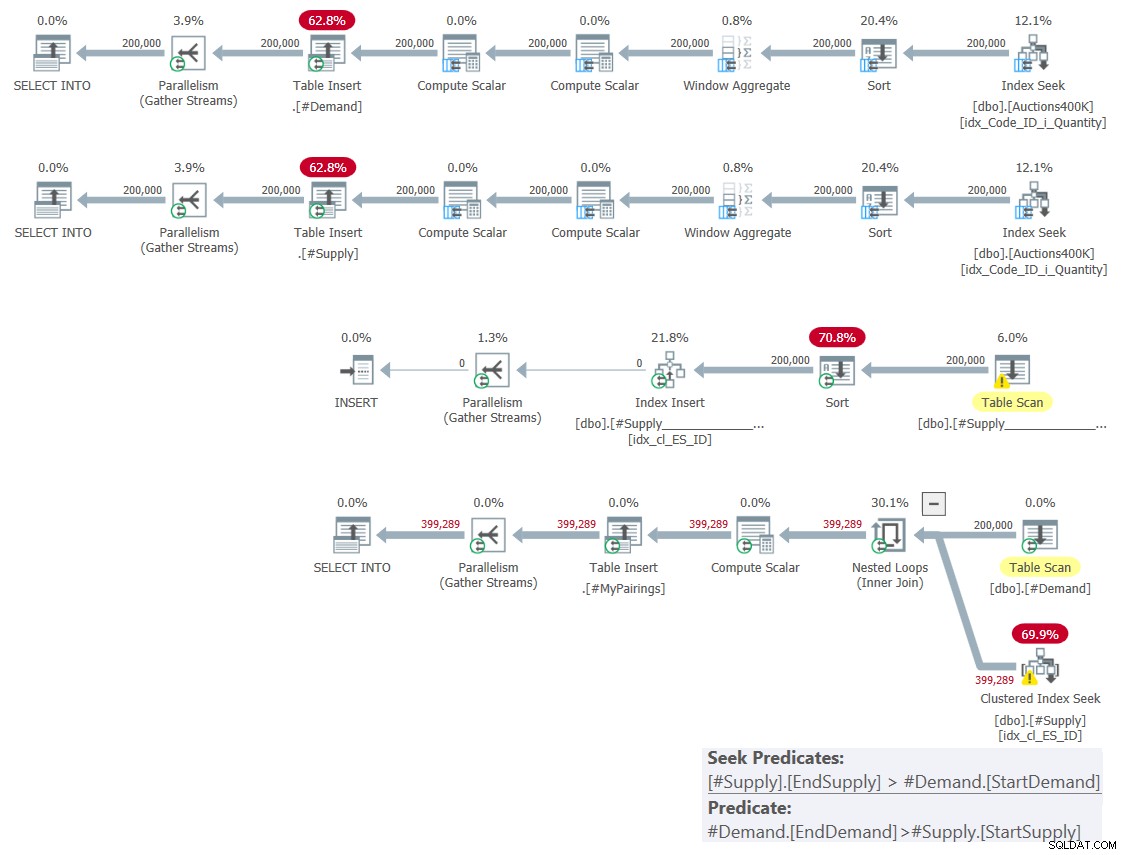Figura 1:piano di query per la soluzione basata sugli incroci classici

Come ho spiegato il mese scorso, tra i due predicati di intervallo coinvolti, solo uno può essere utilizzato come predicato di ricerca nell'ambito di un'operazione di ricerca dell'indice, mentre l'altro deve essere applicato come predicato residuo. Puoi vederlo chiaramente nel piano per l'ultima query nella Figura 1. Ecco perché mi sono preoccupato di creare solo un indice su una delle tabelle. Ho anche forzato l'uso di una ricerca nell'indice che ho creato utilizzando l'hint FORCESESEEK. In caso contrario, l'ottimizzatore potrebbe finire per ignorare quell'indice e crearne uno proprio utilizzando un operatore Index Spool.

Questo piano ha una complessità quadratica poiché per riga in un lato — #Demand nel nostro caso — la ricerca dell'indice dovrà accedere in media a metà delle righe nell'altro lato — #Supply nel nostro caso — in base al predicato di ricerca e identificare il finali applicando il predicato residuo.

Se non ti è ancora chiaro il motivo per cui questo piano ha una complessità quadratica, forse una rappresentazione visiva del lavoro potrebbe essere d'aiuto, come mostrato nella Figura 2.

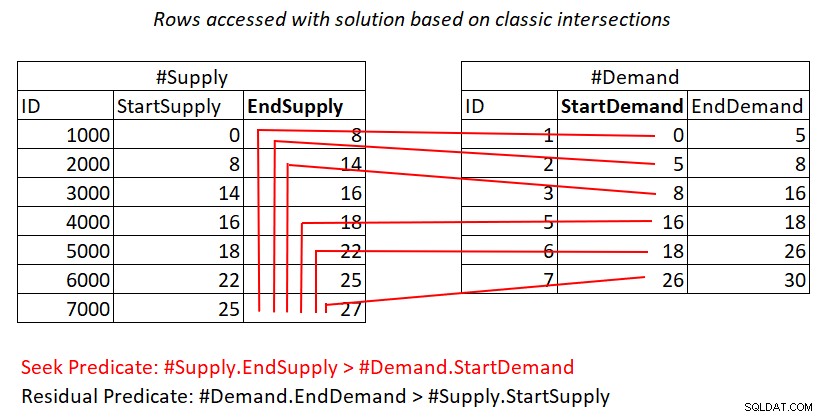Figura 2:Illustrazione del lavoro con una soluzione basata sulle intersezioni classiche

Questa illustrazione rappresenta il lavoro svolto dall'unione di cicli nidificati nel piano per l'ultima query. L'heap #Demand è l'input esterno del join e l'indice cluster su #Supply (con EndSupply come chiave iniziale) è l'input interno. Le linee rosse rappresentano le attività di ricerca dell'indice eseguite per riga in #Demand nell'indice su #Supply e le righe a cui accedono come parte delle scansioni dell'intervallo nella foglia dell'indice. Verso valori di StartDemand estremamente bassi in #Demand, la scansione dell'intervallo deve accedere a quasi tutte le righe in #Supply. Verso valori di StartDemand estremamente alti in #Demand, la scansione dell'intervallo deve accedere a righe vicine a zero in #Supply. In media, la scansione dell'intervallo deve accedere a circa la metà delle righe in #Supply per riga richiesta. Con D righe di domanda e S righe di offerta, il numero di righe a cui si accede è D + D*S/2. Questo è in aggiunta al costo delle ricerche che ti portano alle righe corrispondenti. Ad esempio, quando si riempie dbo.Auctions con 200.000 righe di domanda e 200.000 righe di offerta, ciò si traduce in Nested Loops join che accede a 200.000 righe di domanda + 200.000*200.000/2 righe di offerta o 200.000 + 200.000^2/2 =20.000.200.000 di righe a cui si accede. C'è un sacco di nuove scansioni di file di forniture in corso qui!

Se vuoi attenerti all'idea delle intersezioni a intervalli ma ottenere buone prestazioni, devi trovare un modo per ridurre la quantità di lavoro svolto.

Nella sua soluzione, Joe Obbish ha raggruppato gli intervalli in base alla lunghezza massima dell'intervallo. In questo modo è stato in grado di ridurre il numero di righe che i join dovevano gestire e fare affidamento sull'elaborazione batch. Ha utilizzato il classico test di intersezione a intervalli come filtro finale. La soluzione di Joe funziona bene purché la lunghezza massima dell'intervallo non sia molto elevata, ma il tempo di esecuzione della soluzione aumenta all'aumentare della lunghezza massima dell'intervallo.

Allora, cos'altro puoi fare...?

Test di intersezione rivisto

Luca, Kamil e forse Daniel (c'era una parte poco chiara sulla sua soluzione pubblicata a causa della formattazione del sito Web, quindi dovevo indovinare) hanno utilizzato un test di intersezione dell'intervallo rivisto che consente un utilizzo molto migliore dell'indicizzazione.

Il loro test di intersezione è una disgiunzione di due predicati (predicati separati dall'operatore OR):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

In inglese, il delimitatore di inizio della domanda si interseca con l'intervallo di fornitura in modo inclusivo ed esclusivo (incluso l'inizio e la fine esclusa); oppure il delimitatore di inizio fornitura si interseca con l'intervallo di domanda, in modo inclusivo ed esclusivo. Per rendere i due predicati disgiunti (non avere casi sovrapposti) ma comunque completi nel coprire tutti i casi, puoi mantenere l'operatore =solo nell'uno o nell'altro, ad esempio:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Questo test di intersezione intervallo rivisto è piuttosto perspicace. Ciascuno dei predicati può potenzialmente utilizzare in modo efficiente un indice. Considera il predicato 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Supponendo che tu crei un indice di copertura su #Demand con StartDemand come chiave principale, puoi potenzialmente ottenere un join Nested Loops applicando il lavoro illustrato nella Figura 3.


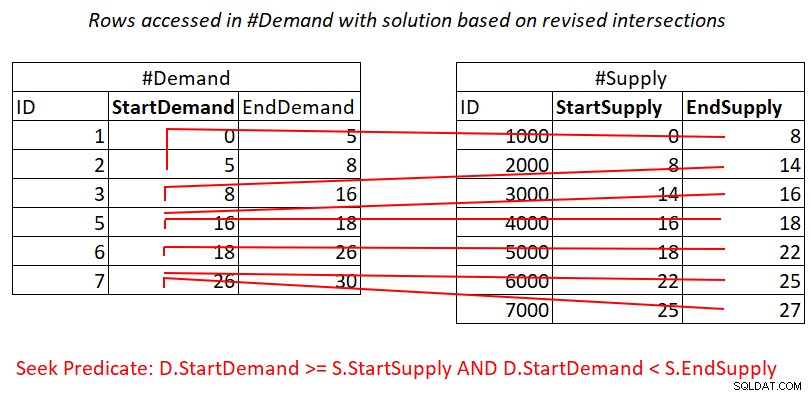
Figura 3:Illustrazione del lavoro teorico richiesto per elaborare il predicato 1

Sì, paghi ancora per una ricerca nell'indice #Demand per riga in #Supply, ma le scansioni dell'intervallo nella foglia dell'indice accedono a sottoinsiemi di righe quasi disgiunti. Nessuna nuova scansione delle righe!

La situazione è simile con il predicato 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Supponendo che tu crei un indice di copertura su #Supply con StartSupply come chiave iniziale, puoi potenzialmente ottenere un join Nested Loops applicando il lavoro illustrato nella Figura 4.


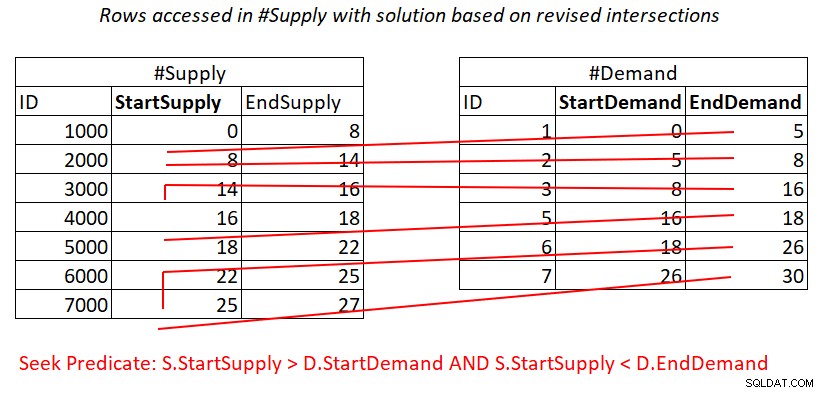
Figura 4:Illustrazione del lavoro teorico richiesto per elaborare il predicato 2

Inoltre, qui paghi per una ricerca nell'indice #Supply per riga in #Demand, quindi l'intervallo esegue la scansione nella foglia dell'indice accede a sottoinsiemi di righe quasi disgiunti. Ancora una volta, nessuna nuova scansione delle righe!

Assumendo D righe di domanda e S righe di offerta, il lavoro può essere descritto come:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Quindi è probabile che la parte più grande del costo qui sia il costo di I/O coinvolto con le ricerche. Ma questa parte del lavoro ha un ridimensionamento lineare rispetto al ridimensionamento quadratico della classica query di intersezioni di intervallo.

Ovviamente, devi considerare il costo preliminare della creazione dell'indice sulle tabelle temporanee, che ha n log n ridimensionamento a causa dell'ordinamento coinvolto, ma paghi questa parte come parte preliminare di entrambe le soluzioni.

Proviamo a mettere in pratica questa teoria. Iniziamo popolando le tabelle temporanee #Demand e #supply con gli intervalli di domanda e offerta (come le classiche intersezioni di intervallo) e creando gli indici di supporto:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

I piani per popolare le tabelle temporanee e creare gli indici sono mostrati nella Figura 5.


Figura 5:piani di query per popolare tabelle temporanee e creare indici

Nessuna sorpresa qui.

Ora alla domanda finale. Potresti essere tentato di utilizzare una singola query con la suddetta disgiunzione di due predicati, in questo modo:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

Il piano per questa query è mostrato nella Figura 6.


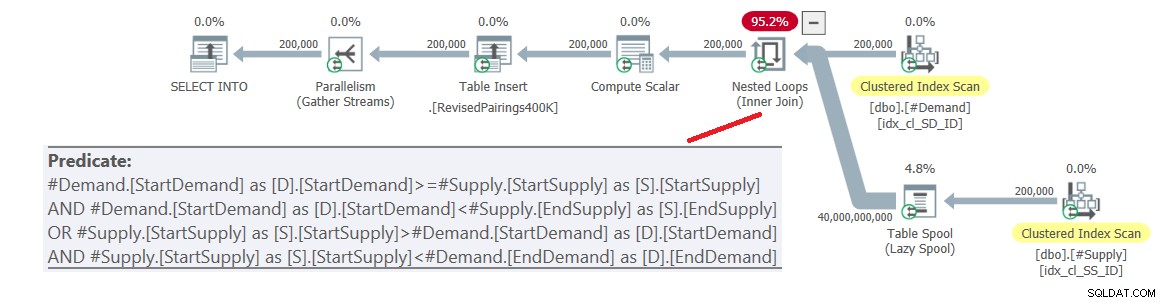
Figura 6:piano di query per la query finale utilizzando l'intersezione rivista prova, prova 1

Il problema è che l'ottimizzatore non sa come suddividere questa logica in due attività separate, ciascuna gestendo un predicato diverso e utilizzando il rispettivo indice in modo efficiente. Quindi, si finisce con un prodotto cartesiano completo delle due parti, applicando tutti i predicati come predicati residui. Con 200.000 righe della domanda e 200.000 righe dell'offerta, il join elabora 40.000.000.000 di righe.

Il trucco perspicace utilizzato da Luca, Kamil e forse Daniel è stato quello di spezzare la logica in due query, unificando i loro risultati. Ecco dove l'uso di due predicati disgiunti diventa importante! Puoi utilizzare un operatore UNION ALL invece di UNION, evitando il costo inutile della ricerca di duplicati. Ecco la query che implementa questo approccio:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Il piano per questa query è mostrato nella Figura 7.


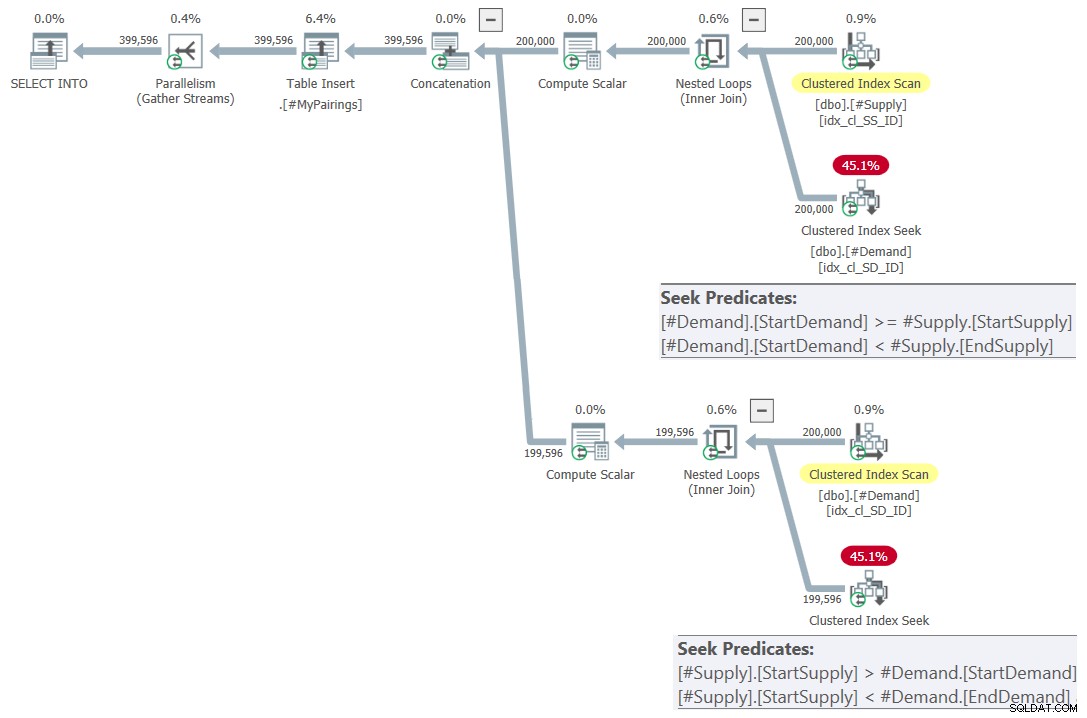
Figura 7:piano di query per la query finale utilizzando l'intersezione rivista prova, prova 2

Questo è semplicemente bellissimo! Non è vero? E poiché è così bello, ecco l'intera soluzione da zero, inclusa la creazione di tabelle temporanee, l'indicizzazione e la query finale:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Come accennato in precedenza, mi riferirò a questa soluzione come a intersezioni riviste .

La soluzione di Kamil

Tra le soluzioni di Luca, Kamil e Daniel, quella di Kamil è stata la più veloce. Ecco la soluzione completa di Kamil:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Come puoi vedere, è molto vicino alla soluzione degli incroci rivista che ho trattato.

Il piano per la query finale nella soluzione di Kamil è mostrato nella Figura 8.


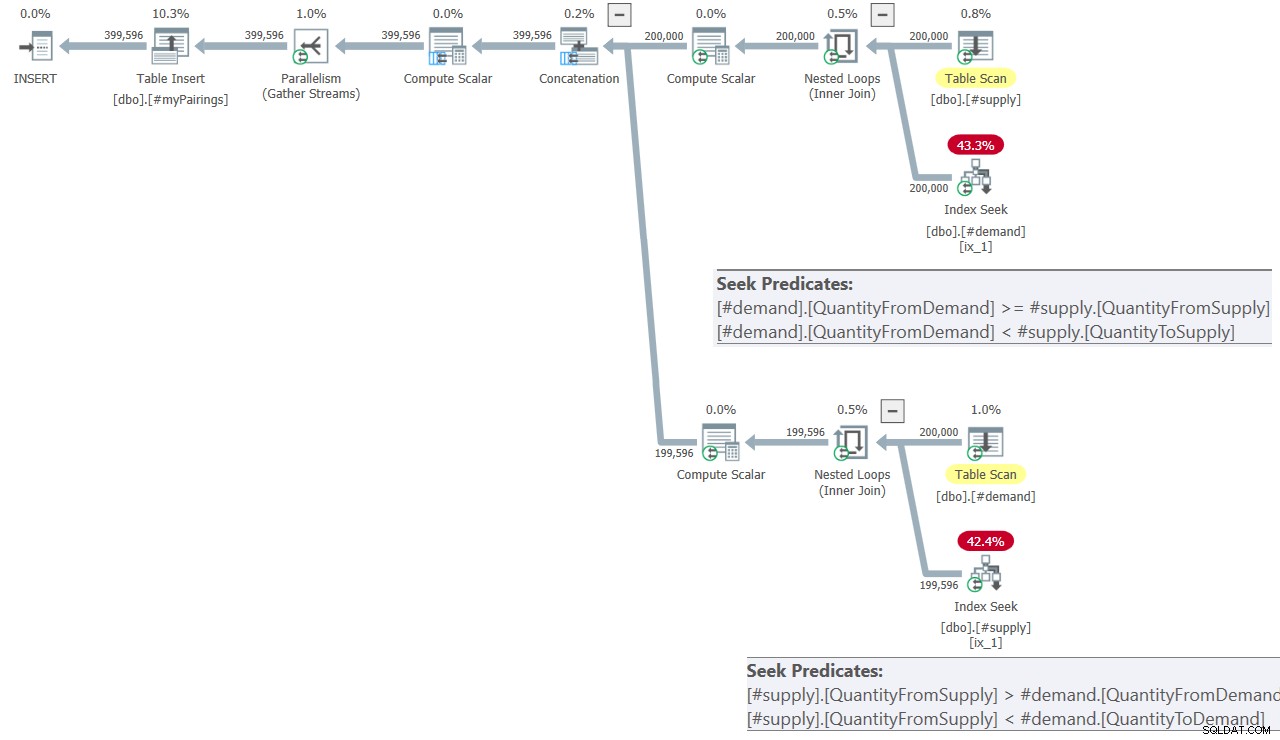
Figura 8:piano di query per la query finale nella soluzione di Kamil

Il piano sembra abbastanza simile a quello mostrato in precedenza nella Figura 7.

Test delle prestazioni

Ricordiamo che la soluzione classica delle intersezioni ha impiegato 931 secondi per essere completata rispetto a un input con 400.000 righe. Sono 15 minuti! È molto, molto peggio della soluzione del cursore, che ha impiegato circa 12 secondi per essere completata con lo stesso input. La figura 9 mostra i numeri delle prestazioni comprese le nuove soluzioni discusse in questo articolo.


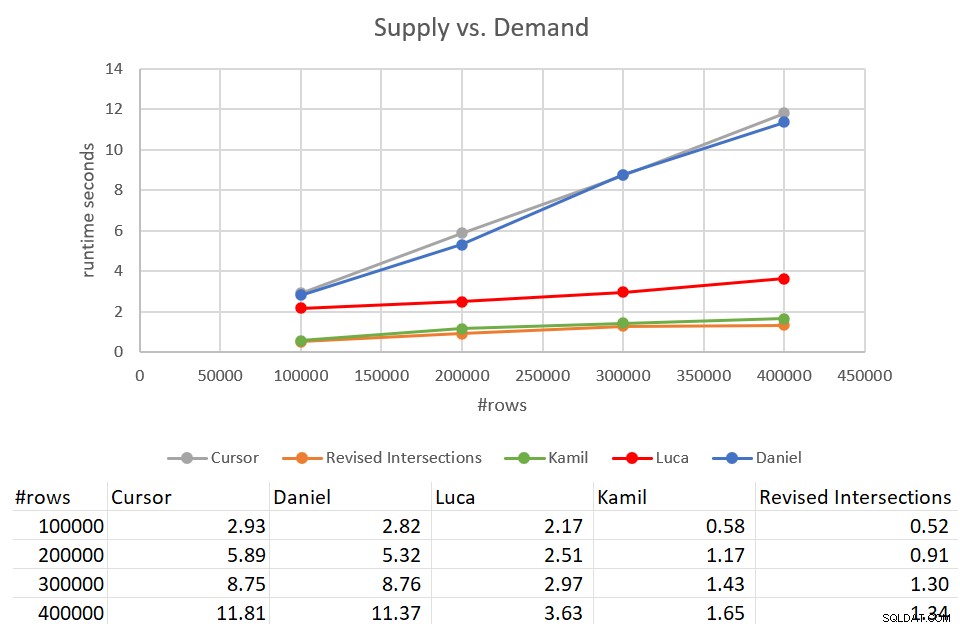
Figura 9:test delle prestazioni

Come puoi vedere, la soluzione di Kamil e la soluzione simile per le intersezioni riviste hanno impiegato circa 1,5 secondi per essere completate rispetto all'input di 400.000 righe. Questo è un miglioramento abbastanza decente rispetto alla soluzione originale basata sul cursore. Lo svantaggio principale di queste soluzioni è il costo di I/O. Con una ricerca per riga, per un input di 400.000 righe, queste soluzioni eseguono un eccesso di 1,35 milioni di letture. Ma potrebbe anche essere considerato un costo perfettamente accettabile dato il buon tempo di esecuzione e il ridimensionamento che ottieni.

Cosa c'è dopo?

Il nostro primo tentativo di risolvere la sfida della corrispondenza tra domanda e offerta si è basato sul classico test di intersezione dell'intervallo e ha ottenuto un piano con prestazioni scadenti con ridimensionamento quadratico. Molto peggio della soluzione basata sul cursore. Sulla base delle informazioni di Luca, Kamil e Daniel, utilizzando un test di intersezione intervallo rivisto, il nostro secondo tentativo è stato un miglioramento significativo che utilizza l'indicizzazione in modo efficiente e offre prestazioni migliori rispetto alla soluzione basata sul cursore. Tuttavia, questa soluzione comporta un costo di I/O significativo. Il mese prossimo continuerò a esplorare soluzioni aggiuntive.

[ Vai a:Sfida originale | Soluzioni:Parte 1 | Parte 2 | parte 3]