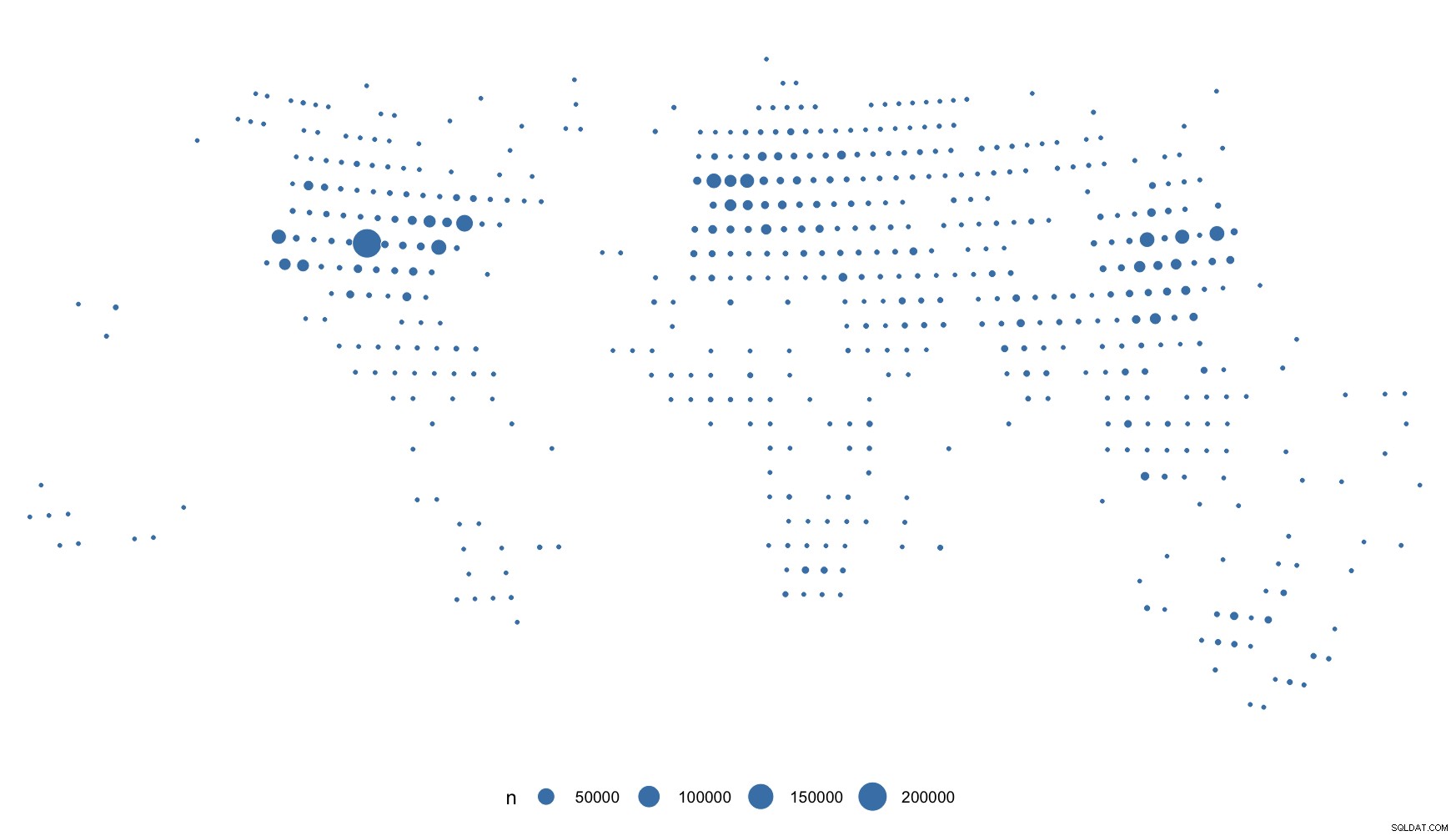
Genereremo alcuni indirizzi IP, geolocalizziamo gli oggetti e li tracciamo:
library(iptools)
library(rgeolocate)
library(tidyverse)
Genera un milione di indirizzi IPv4 casuali (distribuiti in modo troppo uniforme):
ips <- ip_random(1000000)
E geolocalizzali:
system.time(
rgeolocate::maxmind(
ips, "~/Data/GeoLite2-City.mmdb", c("longitude", "latitude")
) -> xdf
)
## user system elapsed
## 5.016 0.131 5.217
5 secondi per 1 milione di IPv4. 👍🏼
Ora a causa dell'uniformità, le bolle saranno stupide piccole, quindi solo per questo esempio le arrotondiamo un po':
xdf %>%
mutate(
longitude = (longitude %/% 5) * 5,
latitude = (latitude %/% 5) * 5
) %>%
count(longitude, latitude) -> pts
E, tracciali:
ggplot(pts) +
geom_point(
aes(longitude, latitude, size = n),
shape=21, fill = "steelblue", color = "white", stroke=0.25
) +
ggalt::coord_proj("+proj=wintri") +
ggthemes::theme_map() +
theme(legend.justification = "center") +
theme(legend.position = "bottom")
Puoi vedere cosa intendo con "troppo uniforme". Ma hai IPv4 "reali", quindi dovresti essere gtg.
Prendi in considerazione l'utilizzo di scale_size_area() , ma, onestamente, considera di non tracciare affatto IPv4 su una mappa geografica. Faccio ricerche su Internet per vivere e le affermazioni sull'accuratezza lasciano molto a desiderare. Raramente vado al di sotto dell'attribuzione a livello di paese per questo motivo (e paghiamo per dati "reali").