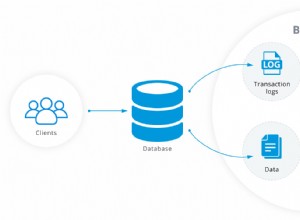
La legge dei coseni e la formula di Haversine daranno risultati identici assumendo una macchina con precisione infinita. La formula Haversine è più robusta per gli errori in virgola mobile. Tuttavia, le macchine odierne hanno una precisione doppia dell'ordine di 15 cifre significative e la legge dei coseni potrebbe funzionare perfettamente per te. Entrambe queste formule presuppongono una terra sferica, mentre la soluzione iterativa di Vicenty (la più accurata) presuppone una terra ellissoidale (in realtà la terra non è nemmeno un ellissoide - è un geoide). Alcuni riferimenti:https://www.movable-type. co.uk/scripts/gis-faq-5.1.html
C'è di meglio:si noti che la latitudine da utilizzare nella legge dei coseni così come l'Harsine è la latitudine geocentrica, che è diversa dalla latitudine geodetica. Per una sfera, questi due sono gli stessi.
Qual è il più veloce da calcolare?
In ordine dal più veloce al più lento sono:legge dei coseni (5 chiamate trig.) -> haversine (coinvolge sqrt) -> Vicenty (devo risolverlo in modo iterativo in un ciclo for)
Qual è il più preciso?
Vicentino.
Qual è il migliore quando si considerano sia la velocità che la precisione?
Se il dominio del tuo problema è tale che per le distanze che stai cercando di calcolare, la terra può essere considerata piatta, allora puoi elaborare (non fornirò dettagli) una formula della forma x =kx * differenza di longitudine , y =ky * differenza di latitudine. Quindi distanza =sqrt(dxdx + dy dio). Se il dominio del tuo problema è tale da poter essere risolto con la distanza al quadrato, non dovrai prendere sqrt e questa formula sarà il più veloce possibile. Ha l'ulteriore vantaggio di poter calcolare il vettore distanza - x è la distanza in direzione est e y è la distanza in direzione nord. Altrimenti, sperimenta con il 3 e scegli ciò che funziona meglio nella tua situazione.