Il mese scorso ho affrontato l'enigma di Peter Larsson di far corrispondere l'offerta con la domanda. Ho mostrato la semplice soluzione basata sul cursore di Peter e ho spiegato che ha un ridimensionamento lineare. La sfida che ti ho lasciato è cercare di trovare una soluzione basata su set per il compito e, ragazzo, fai in modo che le persone siano all'altezza della sfida! Grazie Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie e, naturalmente, Peter Larsson, per aver inviato le vostre soluzioni. Alcune delle idee erano brillanti e assolutamente strabilianti.
Questo mese inizierò a esplorare le soluzioni presentate, approssimativamente, passando da quelle con le prestazioni peggiori a quelle con le migliori prestazioni. Perché anche preoccuparsi di quelli con prestazioni scadenti? Perché puoi ancora imparare molto da loro; ad esempio, identificando gli anti-pattern. In effetti, il primo tentativo di risolvere questa sfida per molte persone, inclusi me e Peter, si basa su un concetto di intersezione di intervallo. Accade così che la classica tecnica basata sui predicati per identificare l'intersezione di intervallo abbia prestazioni scarse poiché non esiste un buon schema di indicizzazione per supportarla. Questo articolo è dedicato a questo approccio con scarse prestazioni. Nonostante le scarse prestazioni, lavorare sulla soluzione è un esercizio interessante. Richiede l'esercizio dell'abilità di modellare il problema in un modo che si presti a un trattamento basato sul set. È anche interessante identificare il motivo della cattiva prestazione, rendendo più facile evitare l'anti-pattern in futuro. Tieni presente che questa soluzione è solo il punto di partenza.
DDL e un piccolo set di dati di esempio
Come promemoria, l'attività prevede l'esecuzione di query su una tabella denominata "Aste". Utilizza il codice seguente per creare la tabella e popolarla con un piccolo insieme di dati di esempio:
DROP TABLE SE ESISTE dbo.Auctions; CREATE TABLE dbo.Auctions( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Auctions PRIMARY KEY CLUSTERED, Code CHAR(1) NOT NULL CONSTRAINT ck_Auctions_Code CHECK (Code ='D' OR Code ='S'), Quantità DECIMAL(19 , 6) VINCOLO NON NULLO ck_Auctions_Quantity CHECK (Quantity> 0)); IMPOSTA NESSUN CONTO ATTIVO; ELIMINA DA dbo.Auctions; SET IDENTITY_INSERT dbo.Auctions ON; INSERT INTO dbo.Auctions(ID, Code, Quantity) VALORI (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2.0); SET IDENTITY_INSERT dbo.Auctions OFF;
Il tuo compito era creare accoppiamenti che corrispondano all'offerta con le voci della domanda in base all'ordinamento degli ID, scrivendole in una tabella temporanea. Di seguito è riportato il risultato desiderato per il piccolo insieme di dati di esempio:
DemandID SupplyID TradeQuantity----------- ----------- --------------1 1000 5.0000002 1000 3.0000003 2000 6.0000003 3000 2.0000005 4000 2.0000006 5000 4.0000006 6000 3.0000006 7000 1.0000007 7000 1.000000
Il mese scorso ho anche fornito un codice che puoi utilizzare per popolare la tabella Aste con un ampio set di dati campione, controllando il numero di voci di domanda e offerta, nonché il loro intervallo di quantità. Assicurati di utilizzare il codice dell'articolo del mese scorso per verificare le prestazioni delle soluzioni.
Modellazione dei dati come intervalli
Un'idea intrigante che si presta a supportare soluzioni basate su insiemi è modellare i dati come intervalli. In altre parole, rappresentare ogni voce di domanda e offerta come un intervallo che inizia con le quantità totali parziali dello stesso tipo (domanda o offerta) fino a ma esclusa la corrente e termina con il totale parziale inclusa la corrente, ovviamente in base all'ID ordinare. Ad esempio, guardando il piccolo insieme di dati campione, la prima voce della domanda (ID 1) è per una quantità di 5,0 e la seconda (ID 2) è per una quantità di 3,0. La prima voce di domanda può essere rappresentata con l'intervallo inizio:0.0, fine:5.0 e la seconda con l'intervallo di inizio:5.0, fine:8.0 e così via.
Allo stesso modo, la prima voce di fornitura (ID 1000) è per una quantità di 8,0 e il secondo (ID 2000) è per una quantità di 6,0. La prima voce di fornitura può essere rappresentata con l'intervallo inizio:0.0, fine:8.0 e la seconda con l'intervallo inizio:8.0, fine:14.0 e così via.
Gli accoppiamenti domanda-offerta che devi creare sono quindi i segmenti sovrapposti degli intervalli di intersezione tra i due tipi.
Questo è probabilmente meglio compreso con una rappresentazione visiva della modellazione basata su intervalli dei dati e del risultato desiderato, come mostrato nella Figura 1.
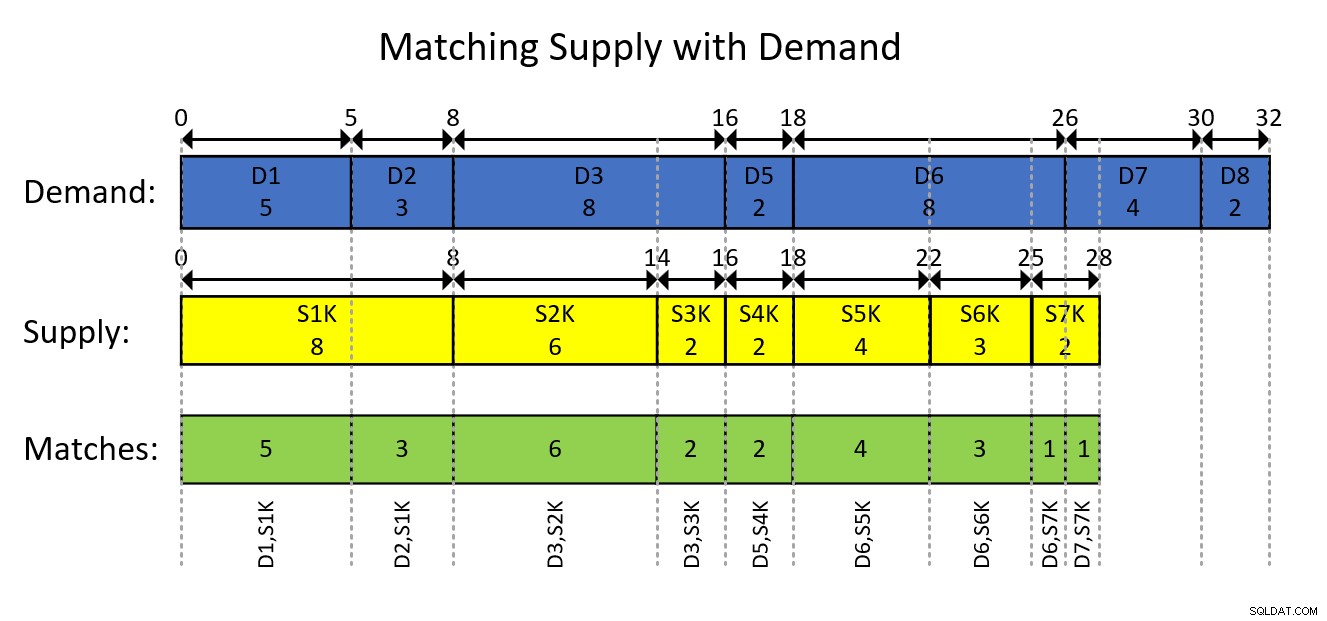Figura 1:modellazione dei dati come intervalli
La rappresentazione visiva nella Figura 1 è abbastanza autoesplicativa ma, in breve...
I rettangoli blu rappresentano le voci della domanda come intervalli, mostrando le quantità del totale parziale esclusivo all'inizio dell'intervallo e il totale parziale compreso alla fine dell'intervallo. I rettangoli gialli fanno lo stesso per le voci di fornitura. Quindi nota come i segmenti sovrapposti degli intervalli intersecanti dei due tipi, che sono rappresentati dai rettangoli verdi, sono gli accoppiamenti domanda-offerta che devi produrre. Ad esempio, il primo abbinamento di risultati è con ID domanda 1, ID fornitura 1000, quantità 5. Il secondo abbinamento di risultati è con ID domanda 2, ID fornitura 1000, quantità 3. E così via.
Intersezioni a intervalli mediante CTE
Prima di iniziare a scrivere il codice T-SQL con soluzioni basate sull'idea di modellazione degli intervalli, dovresti già avere un'idea intuitiva di quali indici potrebbero essere utili qui. Poiché è probabile che tu utilizzi le funzioni della finestra per calcolare i totali parziali, potresti trarre vantaggio da un indice di copertura con una chiave basata sulle colonne Codice, ID e inclusa la colonna Quantità. Ecco il codice per creare un tale indice:
CREA INDICE NON CLUSTERED UNICO idx_Code_ID_i_Quantity SU dbo.Auctions(Code, ID) INCLUDE(Quantity);
È lo stesso indice che ho consigliato per la soluzione basata sul cursore che ho trattato il mese scorso.
Inoltre, qui c'è il potenziale per trarre vantaggio dall'elaborazione batch. Puoi abilitarne la considerazione senza i requisiti della modalità batch su rowstore, ad esempio utilizzando SQL Server 2019 Enterprise o versioni successive, creando il seguente indice columnstore fittizio:
CREA INDEX COLUMNSTORE NON CLUSTERED idx_cs SU dbo.Auctions(ID) DOVE ID =-1 AND ID =-2;
Ora puoi iniziare a lavorare sul codice T-SQL della soluzione.
Il codice seguente crea gli intervalli che rappresentano le voci di domanda:
CON D0 AS-- D0 calcola la domanda in esecuzione come EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D estrae prev EndDemand come StartDemand, esprimendo la domanda inizio-fine come un intervalloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT *FROM D;
La query che definisce il CTE D0 filtra le voci di domanda dalla tabella Aste e calcola una quantità totale parziale come delimitatore finale degli intervalli di domanda. Quindi la query che definisce il secondo CTE denominata D interroga D0 e calcola il delimitatore iniziale degli intervalli di domanda sottraendo la quantità corrente dal delimitatore finale.
Questo codice genera il seguente output:
ID Quantità StartDemand EndDemand---- --------- ------------ ----------1 5.000000 0.000000 5.0000002 3.000000 5.000000 8.0000003 8.000000 8.000000 16.0000005 2.000000 16.000000 18.0000006 8.000000 18.000000 26.0000007 4.000000 26.000000 30.0000008 2.000000 300 3.00Gli intervalli di fornitura sono generati in modo molto simile applicando la stessa logica alle entrate di fornitura, utilizzando il seguente codice:
CON S0 AS-- S0 calcola la fornitura in esecuzione come EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S estrae prev EndSupply come StartSupply, esprimendo la fornitura inizio-fine come un intervalloS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT *DA S;Questo codice genera il seguente output:
ID Quantità InizioSupply FineSupply----- --------- ------------ ----------1000 8.000000 0.000000 8.0000002000 6.000000 8.000000 14.0000003000 2.000000 14.000000 16.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.00006000 3.000000 22.000000 25.0000007000 2.000000 25.000000 27.000000Ciò che resta è quindi identificare gli intervalli di domanda e offerta che si intersecano dai CTE D e S e calcolare i segmenti sovrapposti di quegli intervalli di intersezione. Ricorda che gli accoppiamenti dei risultati devono essere scritti in una tabella temporanea. Questo può essere fatto usando il seguente codice:
-- Elimina la tabella temporanea se esisteDROP TABLE SE ESISTE #MyPairings; CON D0 AS-- D0 calcola la domanda in esecuzione come EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D estrae prev EndDemand come StartDemand, esprimendo la domanda inizio-fine come un intervalloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 calcola l'offerta in esecuzione come EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER (ORDINA PER ID ROWS UNBOUNDED PRECEDENTE) COME EndSupply DA dbo.Auctions WHERE Code ='S'),-- S estrae prev EndSupply come StartSupply, esprimendo inizio-fine fornitura come intervalli AS( SELECT ID, Quantità, EndSupply - Quantità AS StartSupply, EndSupply FROM S0)-- La query esterna identifica gli scambi come segmenti sovrapposti degli intervalli di intersezione-- Negli intervalli di domanda e offerta che si intersecano la quantità commerciale è quindi -- LEAST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WH IT EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsDA D INNER UNISCITI SU D.StartDemand S.StartSupply; Oltre al codice che crea gli intervalli di domanda e offerta, che hai già visto in precedenza, l'aggiunta principale qui è la query esterna, che identifica gli intervalli di intersezione tra D e S e calcola i segmenti sovrapposti. Per identificare gli intervalli di intersezione, la query esterna unisce D e S utilizzando il seguente predicato di join:
D.StartDemandS.StartSupply Questo è il classico predicato per identificare l'intersezione di intervallo. È anche la causa principale delle scarse prestazioni della soluzione, come spiegherò tra breve.
La query esterna calcola anche la quantità commerciale nell'elenco SELECT come:
LEAST(EndDemand, EndSupply) - GREATEST(StartDemand, StartSupply)Se stai usando Azure SQL, puoi usare questa espressione. Se utilizzi SQL Server 2019 o versioni precedenti, puoi utilizzare la seguente alternativa logicamente equivalente:
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END Poiché il requisito era scrivere il risultato in una tabella temporanea, la query esterna utilizza un'istruzione SELECT INTO per ottenere questo risultato.
L'idea di modellare i dati come intervalli è chiaramente intrigante ed elegante. Ma per quanto riguarda le prestazioni? Sfortunatamente, questa soluzione specifica presenta un grosso problema relativo al modo in cui viene identificata l'intersezione degli intervalli. Esaminare il piano per questa soluzione mostrato nella Figura 2.
Figura 2:piano di query per le intersezioni utilizzando la soluzione CTE
Iniziamo con le parti economiche del piano.
L'input esterno del join Nested Loops calcola gli intervalli di domanda. Utilizza un operatore Index Seek per recuperare le voci della domanda e un operatore Window Aggregate in modalità batch per calcolare il delimitatore di fine dell'intervallo di domanda (denominato Expr1005 in questo piano). Il delimitatore di inizio dell'intervallo di domanda è quindi Espr1005 – Quantità (da D).
Come nota a margine, potresti trovare sorprendente l'uso di un operatore di ordinamento esplicito prima dell'operatore Window Aggregate in modalità batch, poiché le voci della domanda recuperate da Index Seek sono già ordinate per ID come la funzione della finestra richiede che siano. Ciò ha a che fare con il fatto che attualmente SQL Server non supporta una combinazione efficiente di operazioni parallele sull'indice di conservazione degli ordini prima di un operatore di Window Aggregate in modalità batch parallela. Se forzi un piano seriale solo a scopo di sperimentazione, vedrai scomparire l'operatore di ordinamento. SQL Server ha deciso nel complesso, l'uso del parallelismo qui è stato preferito, nonostante ciò abbia comportato l'aggiunta dell'ordinamento esplicito. Ma ancora, questa parte del piano rappresenta una piccola parte del lavoro nel grande schema delle cose.
Allo stesso modo, l'input interno del join Nested Loops inizia calcolando gli intervalli di fornitura. Curiosamente, SQL Server ha scelto di utilizzare gli operatori in modalità riga per gestire questa parte. Da un lato, gli operatori in modalità riga utilizzati per calcolare i totali parziali comportano un sovraccarico maggiore rispetto all'alternativa Window Aggregate in modalità batch; d'altra parte, SQL Server ha un'efficiente implementazione parallela di un'operazione di conservazione dell'indice seguita dal calcolo della funzione finestra, evitando l'ordinamento esplicito per questa parte. È curioso che l'ottimizzatore abbia scelto una strategia per gli intervalli di domanda e un'altra per gli intervalli di fornitura. In ogni caso, l'operatore Index Seek recupera le voci di fornitura e la successiva sequenza di operatori fino all'operatore di calcolo scalare calcola il delimitatore di fine dell'intervallo di fornitura (denominato Expr1009 in questo piano). Il delimitatore di inizio dell'intervallo di fornitura è quindi Espr1009 – Quantità (da S).
Nonostante la quantità di testo che ho usato per descrivere queste due parti, la parte veramente costosa del lavoro nel piano è ciò che viene dopo.
La parte successiva deve unire gli intervalli di domanda e gli intervalli di fornitura utilizzando il seguente predicato:
D.StartDemandS.StartSupply Senza un indice di supporto, supponendo gli intervalli di domanda DI e gli intervalli di fornitura SI, ciò comporterebbe l'elaborazione di righe DI * SI. Il piano in Figura 2 è stato creato dopo aver riempito la tabella Aste con 400.000 righe (200.000 voci di domanda e 200.000 voci di offerta). Quindi, senza alcun indice di supporto, il piano avrebbe dovuto elaborare 200.000 * 200.000 =40.000.000.000 di righe. Per mitigare questo costo, l'ottimizzatore ha scelto di creare un indice temporaneo (consultare l'operatore Index Spool) con il delimitatore di fine intervallo di fornitura (Expr1009) come chiave. Questo è praticamente il meglio che potrebbe fare. Tuttavia, questo risolve solo una parte del problema. Con due predicati di intervallo, solo uno può essere supportato da un predicato di ricerca dell'indice. L'altro deve essere gestito utilizzando un predicato residuo. Infatti, puoi vedere nel piano che la ricerca nell'indice temporaneo utilizza il predicato di ricerca Espr1009> Espr1005 – D.Quantity, seguito da un operatore Filter che gestisce il predicato residuo Espr1005> Espr1009 – S.Quantity.
Supponendo che in media il predicato di ricerca isoli metà delle righe di offerta dall'indice per riga di domanda, il numero totale di righe emesse dall'operatore Index Spool ed elaborate dall'operatore Filter è quindi DI * SI / 2. Nel nostro caso, con 200.000 righe della domanda e 200.000 righe dell'offerta, questo si traduce in 20.000.000.000. Infatti, la riga che va dall'operatore Index Spool all'operatore Filter riporta un numero di righe vicino a questo.
Questo piano ha un ridimensionamento quadratico, rispetto al ridimensionamento lineare della soluzione basata sul cursore del mese scorso. Puoi vedere il risultato di un test delle prestazioni confrontando le due soluzioni nella Figura 3. Puoi vedere chiaramente la parabola ben sagomata per la soluzione basata su insiemi.
Figura 3:prestazioni delle intersezioni utilizzando la soluzione CTE rispetto alla soluzione basata su cursore
Intersezioni di intervalli utilizzando tabelle temporanee
Puoi in qualche modo migliorare le cose sostituendo l'uso di CTE per gli intervalli di domanda e offerta con tabelle temporanee e per evitare lo spooling dell'indice, creando il tuo indice sulla tabella temporanea che contiene gli intervalli di fornitura con il delimitatore finale come chiave. Ecco il codice completo della soluzione:
-- Elimina le tabelle temporanee se esistentiDROP TABLE IF EXISTS #MyPairings, #Demand, #Supply; CON D0 AS-- D0 calcola la domanda in esecuzione come EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D estrae prev EndDemand come StartDemand, che esprime la domanda inizio-fine come un intervalloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;WITH S0 AS-- S0 calcola l'offerta in esecuzione come EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDENTE) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S estrae prev EndSupply come StartSupply, esprimendo fornitura inizio-fine come intervalli AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT ID, Quantità, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupplyINTO #SupplyDA S; CREA INDICE CLUSTERED UNICO idx_cl_ES_ID SU #Supply(EndSupply, ID); -- La query esterna identifica gli scambi come segmenti sovrapposti degli intervalli di intersezione-- Negli intervalli di domanda e offerta che si intersecano la quantità commerciale è quindi -- LEAST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsDA #Demand AS D INNER JOIN #Supply AS S WITH (FORCESEEK) ON D.StartDemand S.StartSupply; I piani per questa soluzione sono mostrati nella Figura 4:
Figura 4:piano di query per le intersezioni utilizzando la soluzione di tabelle temporanee
I primi due piani utilizzano una combinazione di operatori Index Seek + Sort + Window Aggregate in modalità batch per calcolare gli intervalli di domanda e offerta e scriverli in tabelle temporanee. Il terzo piano gestisce la creazione dell'indice sulla tabella #Supply con il delimitatore EndSupply come chiave iniziale.
Il quarto piano rappresenta di gran lunga la maggior parte del lavoro, con un operatore di join Nested Loops che corrisponde a ciascun intervallo da #Demand, gli intervalli intersecanti da #Supply. Osservare che anche qui, l'operatore Index Seek si basa sul predicato #Supply.EndSupply> #Demand.StartDemand come predicato di ricerca e #Demand.EndDemand> #Supply.StartSupply come predicato residuo. Quindi, in termini di complessità/ridimensionamento, ottieni la stessa complessità quadratica della soluzione precedente. Paghi solo meno per riga poiché stai utilizzando il tuo indice invece dello spool di indice utilizzato dal piano precedente. Puoi vedere le prestazioni di questa soluzione rispetto alle due precedenti nella Figura 5.
Figura 5:prestazioni delle intersezioni utilizzando tabelle temporanee rispetto ad altre due soluzioni
Come puoi vedere, la soluzione con le tabelle temporanee ha prestazioni migliori di quella con i CTE, ma ha ancora un ridimensionamento quadratico e funziona molto male rispetto al cursore.
Cosa c'è dopo?
Questo articolo ha trattato il primo tentativo di gestire la classica attività di corrispondenza tra domanda e offerta utilizzando una soluzione basata su set. L'idea era quella di modellare i dati come intervalli, abbinare l'offerta con le voci della domanda identificando gli intervalli di domanda e offerta che si intersecano e quindi calcolare la quantità di scambio in base alla dimensione dei segmenti sovrapposti. Sicuramente un'idea intrigante. Il problema principale con esso è anche il classico problema di identificare l'intersezione di intervallo utilizzando due predicati di intervallo. Anche con il miglior indice in atto, puoi supportare solo un predicato di intervallo con una ricerca dell'indice; l'altro predicato di intervallo deve essere gestito utilizzando un predicato residuo. Ciò si traduce in un piano con complessità quadratica.
Quindi cosa puoi fare per superare questo ostacolo? Ci sono diverse idee. Un'idea brillante appartiene a Joe Obbish, di cui puoi leggere in dettaglio nel suo post sul blog. Tratterò altre idee nei prossimi articoli della serie.
[ Vai a:Sfida originale | Soluzioni:Parte 1 | Parte 2 | parte 3]
