Questo articolo esamina la selettività e la stima della cardinalità per i predicati su COUNT(*) espressioni, come si può vedere in HAVING clausole. Si spera che i dettagli siano di per sé interessanti. Forniscono inoltre una panoramica di alcuni degli approcci generali e degli algoritmi utilizzati dallo stimatore di cardinalità.
Un semplice esempio che utilizza il database di esempio AdventureWorks:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
Siamo interessati a vedere come SQL Server ricava una stima per il predicato sull'espressione count in HAVING clausola.
Naturalmente il HAVING la clausola è solo zucchero di sintassi. Avremmo potuto ugualmente scrivere la query utilizzando una tabella derivata o un'espressione di tabella comune:
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
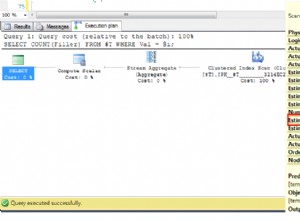
WHERE G.Expr1001 = 1; Tutti e tre i moduli di query producono lo stesso piano di esecuzione, con valori hash del piano di query identici.
Il piano post-esecuzione (effettivo) mostra una stima perfetta per l'aggregato; tuttavia, la stima per il HAVING Il filtro delle clausole (o equivalente, negli altri moduli di query) è scadente:
Statistiche sulla City la colonna fornisce informazioni accurate sul numero di valori di città distinti:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
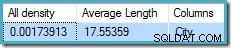
La densità totale figura è il reciproco del numero di valori univoci. Semplice calcolo (1 / 0,00173913) =575 fornisce la stima della cardinalità per l'aggregato. Il raggruppamento per città produce ovviamente una riga per ogni valore distinto.
Tieni presente che tutta la densità deriva dal vettore di densità. Fai attenzione a non utilizzare accidentalmente la densità valore dall'output dell'intestazione delle statistiche di DBCC SHOW_STATISTICS . La densità dell'intestazione viene mantenuta solo per la compatibilità con le versioni precedenti; al giorno d'oggi non viene utilizzato dall'ottimizzatore durante la stima della cardinalità.
Il problema
L'aggregato introduce una nuova colonna calcolata nel flusso di lavoro, denominata Expr1001 nel piano di esecuzione. Contiene il valore di COUNT(*) in ogni riga di output raggruppata:
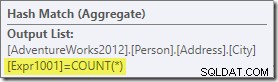
Non ci sono ovviamente informazioni statistiche nel database su questa nuova colonna calcolata. Sebbene l'ottimizzatore sappia che ci saranno 575 righe, non sa nulla della distribuzione di valori di conteggio all'interno di quelle righe.
Beh, non proprio niente:l'ottimizzatore è consapevole che i valori di conteggio saranno interi positivi (1, 2, 3...). Tuttavia, è la distribuzione di questi valori di conteggio intero tra le 575 righe che sarebbe necessaria per stimare accuratamente la selettività di COUNT(*) = 1 predicato.
Si potrebbe pensare che una sorta di informazione sulla distribuzione possa essere derivata dall'istogramma, ma l'istogramma fornisce solo informazioni di conteggio specifiche (in EQ_ROWS ) per i valori dei passi dell'istogramma. Tra i passaggi dell'istogramma, tutto ciò che abbiamo è un riepilogo:RANGE_ROWS le righe hanno DISTINCT_RANGE_ROWS valori distinti. Per le tabelle sufficientemente grandi da tenere a mente la qualità della stima della selettività, è molto probabile che la maggior parte della tabella sia rappresentata da questi riepiloghi intra-step.
Ad esempio, le prime due righe di City istogramma della colonna sono:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

Questo ci dice che c'è esattamente una riga per "Abingdon" e altre 29 righe dopo "Abingdon" ma prima di "Ballard", con 19 valori distinti in quell'intervallo di 29 righe. La query seguente mostra l'effettiva distribuzione delle righe tra valori univoci nell'intervallo intra-step di 29 righe:
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

Ci sono 29 righe con 19 valori distinti, proprio come diceva l'istogramma. Tuttavia, è chiaro che non abbiamo basi per valutare la selettività di un predicato sulla colonna conteggio in quella query. Ad esempio, HAVING COUNT_BIG(*) = 2 restituirebbe 5 righe (per Alexandria, Altadena, Atlanta, Augusta e Austin) ma non abbiamo modo di determinarlo dall'istogramma.
Un'ipotesi plausibile
L'approccio adottato da SQL Server è quello di presumere che ogni gruppo sia molto probabile per contenere il numero medio (medio) complessivo di righe. Questa è semplicemente la cardinalità divisa per il numero di valori univoci. Ad esempio, per 1000 righe con 20 valori univoci, SQL Server presume che (1000 / 20) =50 righe per gruppo sia il valore più probabile.
Tornando al nostro esempio originale, ciò significa che è "molto probabile" che la colonna del conteggio calcolato contenga un valore intorno a (19614/575) ~=34.1113 . Dalla densità è il reciproco del numero di valori unici, possiamo anche esprimerlo come cardinalità * densità =(19614 * 0,00173913), dando un risultato molto simile.
Distribuzione
Dire che il valore medio è molto probabilmente ci porta solo così lontano. Dobbiamo anche stabilire esattamente quanto sia probabile; e come cambia la probabilità man mano che ci allontaniamo dal valore medio. Supponendo che tutti i gruppi abbiano esattamente 34.113 righe nel nostro esempio non sarebbe un'ipotesi molto "educata"!
SQL Server gestisce questo presupponendo una distribuzione normale. Questo ha la caratteristica forma a campana che potresti già conoscere (immagine dalla voce Wikipedia collegata):
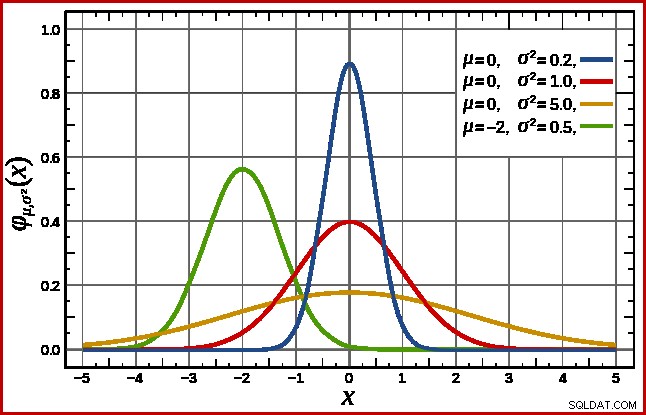
La forma esatta della distribuzione normale dipende da due parametri :la media (µ ) e la deviazione standard (σ ). La media determina la posizione del picco. La deviazione standard specifica quanto è "appiattita" la curva a campana. Più la curva è piatta, più basso è il picco e più la densità di probabilità è distribuita su altri valori.
SQL Server può derivare la media da informazioni statistiche come già notato. La deviazione standard dei valori della colonna di conteggio calcolati è sconosciuto. SQL Server lo stima come radice quadrata della media (con un leggero aggiustamento dettagliato più avanti). Nel nostro esempio, questo significa che i due parametri della distribuzione normale sono approssimativamente 34,1113 e 5,84 (la radice quadrata).
Lo standard la distribuzione normale (la curva rossa nel diagramma sopra) è un caso speciale degno di nota. Ciò si verifica quando la media è zero e la deviazione standard è 1. Qualsiasi distribuzione normale può essere trasformata nella distribuzione normale standard sottraendo la media e dividendo per la deviazione standard.
Aree e intervalli
Siamo interessati a stimare la selettività, quindi stiamo cercando la probabilità che la colonna calcolata del conteggio abbia un certo valore (x). Questa probabilità non è data dal valore dell'asse y sopra, ma dall'area sotto la curva a sinistra di x.
Per la distribuzione normale con media 34,1113 e deviazione standard 5,84, l'area sotto la curva a sinistra di x =30 è di circa 0,2406:
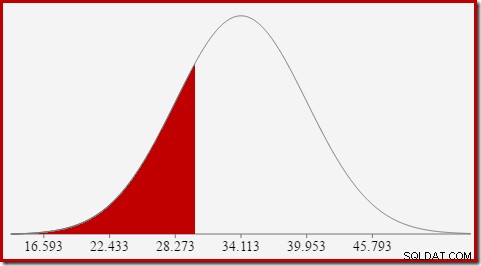
Ciò corrisponde alla probabilità che la colonna del conteggio calcolato sia minore o uguale a 30 per la nostra query di esempio.
Questo porta bene all'idea che in generale non stiamo cercando la probabilità di un valore specifico, ma un intervallo . Per trovare la probabilità che il conteggio uguale un valore intero, dobbiamo tenere conto del fatto che i numeri interi si estendono su un intervallo di dimensione 1. Il modo in cui convertiamo un numero intero in un intervallo è alquanto arbitrario. SQL Server gestisce questo aggiungendo e sottraendo 0,5 per dare i limiti inferiore e superiore dell'intervallo.
Ad esempio, per trovare la probabilità che il valore di conteggio calcolato sia uguale a 30, dobbiamo sottrarre l'area sotto la curva di distribuzione normale per (x =29,5) dall'area per (x =30,5). Il risultato corrisponde alla fetta per (29,5
L'area della fetta rossa è di circa 0,0533 . Con una buona prima approssimazione, questa è la selettività di un predicato count =30 nella nostra query di test.
Calcolare l'area sotto una distribuzione normale a sinistra di un dato valore non è semplice. La formula generale è data dalla funzione di distribuzione cumulativa (CDF). Il problema è che la CDF non può essere espressa in termini di funzioni matematiche elementari, quindi è necessario utilizzare metodi di approssimazione numerica.
Poiché tutte le distribuzioni normali possono essere facilmente trasformate nella distribuzione normale standard (media =0, deviazione standard =1), tutte le approssimazioni funzionano per stimare la normale standard. Ciò significa che dobbiamo trasformare il nostro intervallo delimita dalla distribuzione normale particolare appropriata alla query, alla distribuzione normale standard. Questo viene fatto, come accennato in precedenza, sottraendo la media e dividendo per la deviazione standard.
Se hai dimestichezza con Excel, potresti conoscere le funzioni DISTRIB.NORM. e DISTRIB.NORM.S. che possono calcolare CDF (usando metodi di approssimazione numerica) per una particolare distribuzione normale o la distribuzione normale standard.
Non esiste un calcolatore CDF integrato in SQL Server, ma possiamo facilmente crearne uno. Dato che il CDF per la distribuzione normale standard è:
…dove erf è la funzione di errore:
Di seguito è mostrata un'implementazione T-SQL per ottenere il CDF per la distribuzione normale standard. Utilizza un'approssimazione numerica per la funzione di errore che è molto vicino a quello utilizzato internamente da SQL Server:
Un esempio, per calcolare la CDF per x =30 utilizzando la distribuzione normale per la nostra query di test:
Notare il passaggio di normalizzazione per la conversione alla distribuzione normale standard. La procedura restituisce il valore 0,2407196…, che corrisponde al risultato di Excel corrispondente con sette cifre decimali.
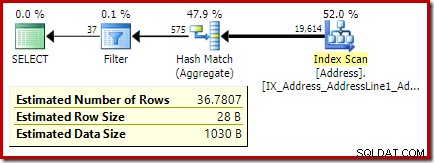
Il codice seguente modifica la nostra query di esempio per produrre una stima più ampia per il filtro (il confronto è ora con il valore 32, che è molto più vicino alla media di prima):
La stima dell'ottimizzatore ora è 36,7807 .
Per calcolare manualmente la stima, dobbiamo prima affrontare alcuni dettagli finali:
La procedura seguente incorpora tutti i dettagli in questo articolo. Richiede la procedura CDF data in precedenza:
Ora possiamo utilizzare questa procedura per generare una stima per la nostra nuova query di test:
L'output è:
Questo si confronta molto bene con la stima della cardinalità dell'ottimizzatore di 36,7807.
La procedura può essere utilizzata per altri intervalli di conteggio oltre ai test di uguaglianza. Tutto ciò che serve è impostare il
Per usarlo con la nostra procedura, impostiamo
Il risultato è 572.5964:
Un ultimo esempio usando
La stima dell'ottimizzatore è
Dal momento che
Anche in questo caso, ciò concorda con la stima dell'ottimizzatore.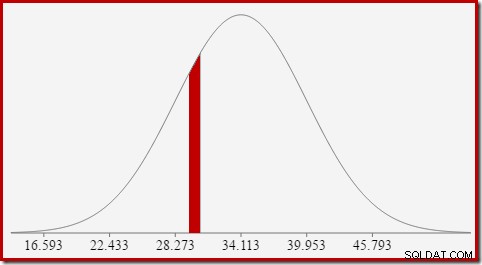
La funzione di distribuzione cumulativa
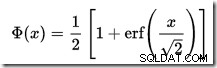
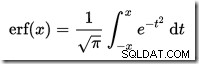
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; Dettagli finali ed esempi
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1 , che qui non è dettagliato. COUNT(*) = 1 caso, il CE legacy utilizza la stessa logica del nuovo CE (disponibile da SQL Server 2014 in poi).CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
Esempi di intervallo di disuguaglianza
@From e @To parametri ai limiti dell'intervallo intero. Per specificare illimitato, passa zero o NULL come preferisci.SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULL e @To = 49 (perché 50 è escluso da meno di):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEEN :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN è inclusivo, passiamo la procedura @From = 25 e @To = 30 . Il risultato è: