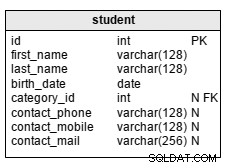
Penso che la tua domanda dica che hai la city valori per le due città tra le quali desideri calcolare la distanza.
Questa query farà il lavoro per te, producendo la distanza in km. Utilizza la formula della legge del coseno sferico.
Nota che unisci la tabella a se stessa in modo da poter recuperare due coppie di coordinate per il calcolo.
SELECT a.city AS from_city, b.city AS to_city,
111.111 *
DEGREES(ACOS(LEAST(1.0, COS(RADIANS(a.Latitude))
* COS(RADIANS(b.Latitude))
* COS(RADIANS(a.Longitude - b.Longitude))
+ SIN(RADIANS(a.Latitude))
* SIN(RADIANS(b.Latitude))))) AS distance_in_km
FROM city AS a
JOIN city AS b ON a.id <> b.id
WHERE a.city = 3 AND b.city = 7
Nota che la costante 111.1111 è il numero di chilometri per grado di latitudine, basato sulla vecchia definizione napoleonica del metro come un decimillesimo della distanza dall'equatore al polo. Quella definizione è abbastanza vicina per il lavoro di ricerca della posizione.
Se vuoi miglia statutarie invece di chilometri, usa 69.0 invece.
https://sqlfiddle.com/#!9/21e06/412/0
Se stai cercando punti nelle vicinanze potresti essere tentato di usare una clausola simile a questa:
HAVING distance_in_km < 10.0 /* slow ! */
ORDER BY distance_in_km DESC
Cioè (come diciamo vicino a Boston MA USA) malvagio lento.
In tal caso è necessario utilizzare un calcolo del riquadro di delimitazione. Vedi questo articolo su come farlo. https://www.plumislandmedia.net/mysql/harsine-mysql- loc-più vicino/
La formula contiene un LEAST() funzione. Come mai? Perché ACOS() La funzione genera un errore se il suo argomento è anche leggermente maggiore di 1. Quando i due punti in questione sono molto vicini tra loro, l'espressione con COS() e SIN() i calcoli a volte possono produrre un valore leggermente maggiore di 1 a causa di epsilon a virgola mobile (imprecisione
). Il LEAST(1.0, dirty-great-expression) call risolve questo problema.
C'è un modo migliore, una formula
di Thaddeus Vincenty
. Usa ATAN2() anziché ACOS() quindi è meno suscettibile ai problemi di epsilon.